Complex Systems Summer School 2012-Projects & Working Groups
From Santa Fe Institute Events Wiki
| Complex Systems Summer School 2012 |
Project proposals
Nonequilibrium game theory
My hope is to adapt some SFI-based models, by people like Crutchfield and Farmer, so that they will quantitatively or qualitatively reproduce features of real human data. Of course, that is very specific, and I'm up for all kinds of ideas in the areas of game learning, game dynamics, small group collective behavior, cognitive science, nonlinear time series, non-eq time series, etc., etc.
Meet me, Seth Frey, at dinner on Thursday and Friday.
Enzyme kinetics – Do enzymes just accelerate equilibrium or play an active role in chemical reactions?
Enzyme networks (e.g. glycolysis) and catalysts in complex mixtures (e.g. Belusov-Zhabotinski reaction) can profoundly influence the outcome of a chemical reaction system. What about a single enzyme? Biochemistry textbooks uniformly say that an enzyme accelerates a reaction without altering its outcome. Yet, the set of differential equations that generically describes enzyme catalysis has remarkable resemblance to the Roessler equations (a textbook example of a non-linear, complex system). With a fixed substrate input or a steady substrate flow, a single enzyme probably cannot affect the reaction outcome. However, sinusoidal or pulsating substrate input, substrate activation or product inhibition, coupling of two enzymes could turn the reaction pattern non-linear. For this project, the sets of equations to study are quite well established – they need to be analyzed. In contrast to some of the more ambitious ideas circulated, this task is exhaustively doable in less than four weeks.
I am Georg Weber. If you are interested in studying this problem, please find me on Tuesday over lunch or dinner (or talk to me at any other unstructured time).
Traffic pattern analysis - Can we estimate car velocity by only observing car counts?
Problem statement
Imagine you have a monitored highway section with a start and end point. At both points you count the number of cars that pass by. The question I'd like to answer / simulate / estimate is: can we make some inference about the velocity of cars although we only have their counts? This would be very useful from an engineering / economic perspective because it's much easier / cheaper to count cars instead of actually tracking them from A to B.
Ideas on how to approach this
I have some intuition about how to go about this, but these are purely statistical (think of it as birth and death process; or as particles in a system that have a certain lifetime - cars in the highway section are like particles in a system, and their velocity is just inverse proportional to their lifetime in this highway section). I would like to see if using explicit physical modeling of motion and agent-based modeling of traffic flow could shed more light on this problem.
Update 06/05/12: Just today we saw Takens theorem about how we can infer a systems structure from only observing a subset of variables. Well, it seems like that's exactly what this project is about.
If you are interested to see more about this check out the SFI Project subsection on Georg M. Goerg or email me to my_3_initials_in_lowercase@stat.cmu.edu. Let's say we meet on Wednesday for lunch (or just ask me any other time you see me around).
Cultural Evolution - General Meet-up
Attention anyone who is interested in cultural evolution or applying your models/methodologies to this fabulous topic!
Let's meet at 4:15 (June 5th) in the cafe during the first "Time to work on Projects" slot. A bunch of us coalesced there tonight and figured we should all properly meet up and then bud off into different projects. Please post your potential buds below:
Cultural Evolution - things that look like drift but aren't
Lots of cultural evolution looks like drift (Bently et al 2004 'Random drift and culture change"). But what social transmission or cognitive learning mechanisms are isomorphic to random sampling with replacement from cultural inputs? In biological evolution, drift serves as a null model of sorts - one that should be ruled out before you can claim that anything more interesting is happening. However, it's not clear what the "uninteresting" type of change is for things that replicate by passing through human cognition and human social systems - like culture does. Is there even a reasonable equivalent of drift in cultural transmission? How should we go about conceptualizing and modeling the evolutionary forces at play in culture?
One candidate for a drifty-lookin' human behavior is probability matching: when people reproduce similar distributions of variation to that which they've learned from. And probability matching is rampant in human behavior (from language learning, to decision making, and even at the neural level). But I think this is a clearly different process than drift, however it still may qualify under Bentley's vague criteria - we can test that out. And there have got to be more drift-esque processes, anyone have any ideas?
If you're interested in these issues or modeling evolution (of any type of system), please give me a shout!
Vanessa
vanferdi [at] gmail.com
"Small Steps and Big Ideas" Group
Christa Dan Xin and Tom spent a while talking after dinner about a bunch of big ideas. Some things we thought about were *big data type network problems, *integrating qualitative social information with models of physical systems, *using games to understand cooperation and decision making.
We'll meet at dinner at 5:30 today (Tuesday, June 5th) in the cafeteria.
107 Proteins in 10-15 cubic meters
Cells rely on proteins to perform vital metabolic and signaling functions; however, it is unclear how proteins are successfully directed to their necessary cellular location(s) in a densely-packed macromolecular environment within the cytoplasm and on the cellular membrane in a short timescale (see for example Weigel et al., PNAS 2011). Using the cell as a manipulatable model of complexity, one could begin to define the parameters and questions, as they pertain to prokaryotic and eukaryotic cells. If interested, please drop me a line: Sepehr Ehsani; sepehr.ehsani[at]utoronto.ca.
Innovation and Technological Progress
I noticed that a number of people mentioned that they were interested in some way in relation to innovation. I was wondering if anyone was interested in a project looking at how particular technologies progress over time and whether charting the form of successful (and/or unsuccessful) previous technologies such as the transistor, fission reactor, mobile phone, etc. in terms of either price, efficiency, or some other variable may be useful in predicting whether a current technology such as solar PV, fuel cell, or something else is following a similar trajectory. Other possible ideas might be to look at using patent, publication, or collaboration network data to reveal certain features of innovation that are not captured by other statistics, particularly for technologies that have yet to reach the market. SFI Professor Doyne Farmer has looked at some of this already in 'The Role of Design Complexity in Technology Improvement', see link: http://adsabs.harvard.edu/abs/2009arXiv0907.0036M
This could be a jumping off point for some ideas on data, methods, models etc. Just throwing the idea out there and it's welcome to completely change but if you're interested, message me (Gareth Haslam) haslam@ias.unu.edu or find me in class.
Space, Stochasticity, Stability; Speciation?
Xue, Chloe and Xiaoliare all working in ecosystems that experience_ a lot of unpredictability in a limiting ecosystem variables (water and/or nutrients); we see patchiness in space and time in how organisms are arranged; and we have some ideas about how the stochasticity may cause the spatial arrangements. Si is working on the stability and robustness of ecosystems.
With enough time, this is likely to involve speciation either to express different strategies, or as a result of spatial separation.
Find any of us walking-around, or meet in the cafeteria at 4:15 June 5th.
Plasticity in Neural Networks
I've done some modeling which shows that the amount of genetic variation that accumulates at any particular metabolic gene (enzyme) in a population at any given time is a function of the network topology in which the gene is embedded, as well as the distance of the network output from an optimum. So, for instance, in a linear metabolic network, enzymes at the beginning of a pathway will tend to be more constrained (show less variation in the population) than at the end of the pathway. This makes sense given that any changes in those first genes would ripple through the system and have a greater relative effect than mutations in later genes. However, this is only true when a population is already close to an optimum. When far from an optimum, we see the exact opposite trend with more variation in the front of the pathway. This also makes sense - when far from a goal, taking bigger steps gives individuals a better chance of achieving higher fitness. The system as a whole then uses the different relative step sizes according to pathway position to "fine tune" its output. I think these findings are quite general - at least the model we used was simple enough that it could apply to many different types of directional developmental processes. We can conceptualize these "genes" more generally as sequential steps in a developmental process with some arbitrary goal. These could be steps in a factory assembly line, major product revisions versus minor releases, or (and this is my favorite), neurons learning about their environment. I'm curious what would happen if we took a similar approach to model neural networks. Genetic variation is the raw material for evolution while neural plasticity is the raw material for learning. The question we would be trying to answer is where, within a neural network, would we expect the most plasticity given a particular network topology and distance form a learning goal. Please contact me (Mark Longo) if this sounds interesting. I'll be available during unstructured time, or you can email mlongo@stanford.edu. [1]
Robustness of complex networks
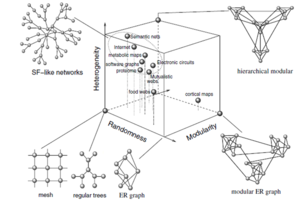
Problem statement
Complex networks have various properties which can be measured in real networks (WWW, social networks, biological networks), e.g. degree distribution, modularity, hierarchy, assortativity etc. Robustness of complex networks is a big question, however only some progress have been done in this direction. For example, it was shown that the scale-free networks are much more topologically robust to random attacks than random networks. Many people claim that various characteristics of complex networks will influence the robustness interdependently. The question I am interested in is how?
Approach
The idea is to generate continuous topology space of various complex networks (networks with different modularity, degree distribution, hierarchy etc) and use it to measure their robustness (see Fig. 1). There are many approaches to measure the robustness of complex networks. For example we can remove edges of vertices of a complex network graph and look at the size of a giant cluster. We can discuss other possibilities.
If you are interested you can contact me directly or via my E-mail: krystoferivanov@gmail.com or via my discussion page in CSSS 2012 wiki.
Relevant literature
- BA Scale-free network
- How to generate Scale-free modular network using preferential attachment
- Error and attack tollerance of complex networks
- Hierarchical organization in complex networks
- Scale-free networks with tunable degree distribution exponents
- Kroneker Graphs
- Add a relevant paper...
Systemic Risk in Financial Networks and/or an ABM of money/liquidity
Systemic Risk in Financial Networks: Hypothesis: the motive to diversify risk at the level of the individual agent (i.e., for an agent to increase its connectivity) will increase systemic risk (by systemic risk I mean vulnerability of the system to widespread collapse). Point of departure is the Forest Fire model from statistical physics.
Key difference(s) between the physics version of the Forest Fire model, and the "economics" version of the Forest Fire model I have in mind are:
- Tree growth probability (which determines network structure) must be endogenous. Agents must be able to choose which other agents to link with.
- Probability of lightning strikes (i.e., defaults on specific loans) must also be endogenous.
I think that financial networks might exhibit self-organizing criticality in the sense that diversification will reduce the probability of lightning strikes (i.e., defaults), however over time systemic risk builds up as a result of the diversification which means that eventually a small number of lightning strikes might be enough to bring the entire system down.
ABM of the emergence of Money: Basically, I would be interested in building an ABM of the emergence of money based around the following economic models of money developed by Nobu Kiyotaki and John Moore:
- [www.princeton.edu/~kiyotaki/papers/Evilistherootofallmoney.pdf Evil is the Root of all Money]
- [www.princeton.edu/~kiyotaki/papers/Financial-Deepening.pdf Financial Deepening]
These models take a broad view of money: "money" is any asset which is widely accepted as a medium of exchange. In these models agents manage projects which require capital investment now in order to generate a return at some point in the future and agents must trade financial promises (think debt contracts) in order to obtain the needed investment. Two key parameters of is these models (which are assumed COMMON to all agents in the above models in order to maintain analytical tractibility) are 0 < theta < 1 and 0 < phi < 1. Theta is the fraction of the future return from the project that an agent can promise to repay in the future in exchange for investment now. Phi is the fraction of the face value of a debt contract (which by construction is a contract between two agents) that can be re-sold to a third agent.
Hypothesis: In an ABM where agents differ in terms of both theta and phi, the promises of only a small number of agents will be widely traded (i.e., will serve as money).
If anyone might be interested in working on these projects, send me and email: drobert.pugh at gmail dot com
Price-time dynamics of contracts traded on prediction markets
Prediction markets have been shown to outperform traditional methods of polls and opinion surveys in forecasting future events. I am interested in exploring the price-time dynamics of contracts traded on prediction markets to better understand how they are able to aggregate individual opinion to establish collective insight.
Several questions that I’m curious to probe further:
- How do ‘information shocks’ generated by news sources influence price-time trajectories?
- Can features of the underlying dynamics be characterized using a simple model?
- What is the minimum number of traders required for an accurate prediction?
On a separate note, I invite you to share your opinion regards whether “China will win the most medals at the 2012 London Olympics”, by logging into the following site (please send me your email address and I will send you the login details).
If you haven't used a prediction market before don't worry -just follow the instructions provided in the site to 'buy' and 'sell' contracts according to your expectation.
If you are interested in the discussing any of the above questions or have other ideas related to prediction markets please get in touch with me at: sanith at mitre dot org
