Modeling gossip networks: Difference between revisions
From Santa Fe Institute Events Wiki
| (32 intermediate revisions by 3 users not shown) | |||
| Line 171: | Line 171: | ||
When we account for initial clustering, the effect of gossip does not appear to differ among network types (Table 1). We only find that gossip tends to destroy links and weaken clustering to a lesser degree in large networks. Furthermore, when the gossip originator is the victim’s weakest link, average degree and clustering are lower compared to the case when the originator is randomly chosen from the victim’s links. This is so because, as elaborated in the analysis, under this rule weaker links become more likely to be severed. | When we account for initial clustering, the effect of gossip does not appear to differ among network types (Table 1). We only find that gossip tends to destroy links and weaken clustering to a lesser degree in large networks. Furthermore, when the gossip originator is the victim’s weakest link, average degree and clustering are lower compared to the case when the originator is randomly chosen from the victim’s links. This is so because, as elaborated in the analysis, under this rule weaker links become more likely to be severed. | ||
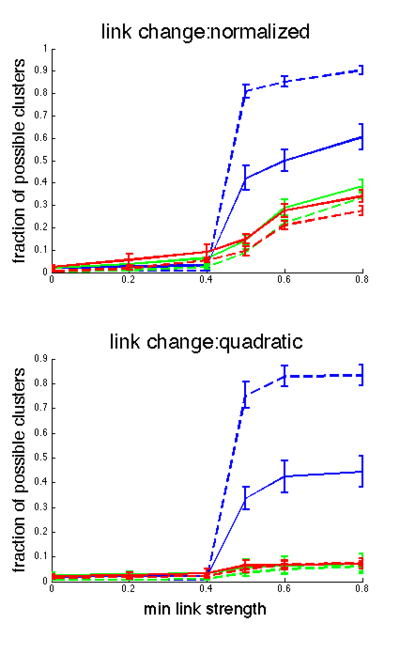
We also looked at network structure as a function of minimum link strength (only including links stronger than this 'min link strength' value for the analysis). | We also looked at network structure as a function of minimum link strength (only including links stronger than this 'min link strength' value for the analysis). Clustering coefficient varies little with min link strength (Fig. 6). Network type influences clustering coefficient more than network size (lines are clustered by color in Fig. 6). In contrast, the fraction of clusters varies greatly with min link strength, and seems to be influenced more by network size than network type. (Fig. 7). Random networks become especially fractured as a function of min link strength. In most cases, both metrics show the largest jump in value between 0.4 and 0.5. We believe this is due to the fact that there are likely many links in the network that are never affected by gossip over the course of the simulations, and stay at their initial 0.5 strength. | ||
Clustering coefficient varies little with min link strength (Fig. 6 | |||
The link change rule also influences both of these network metrics. With the quadratic method, most links converge quickly to 0 or 1, leaving few links of intermediate strength. This is demonstrated by the fact that the results for the quadratic method for both methods are flat as a function of min link strength (except the discontinuity at 0.5 mentioned above). In contrast, the normalized link change method results in links that are more uniformly distributed in strength. Hence, the clustering coefficient is not flat as a function of min link strength (Fig. 6, top panel), and the fraction of possible clusters increases as a function of min link strength (Fig. 7, top panel). | The link change rule also influences both of these network metrics. With the quadratic method, most links converge quickly to 0 or 1, leaving few links of intermediate strength. This is demonstrated by the fact that the results for the quadratic method for both methods are flat as a function of min link strength (except the discontinuity at 0.5 mentioned above). In contrast, the normalized link change method results in links that are more uniformly distributed in strength. Hence, the clustering coefficient is not flat as a function of min link strength (Fig. 6, top panel), and the fraction of possible clusters increases as a function of min link strength (Fig. 7, top panel). | ||
| Line 254: | Line 253: | ||
** Allison: sorry about that, I've fixed them and emailed you new ones. | ** Allison: sorry about that, I've fixed them and emailed you new ones. | ||
* Roozbeh to Allison: <b>Fig. 5</b>, although the format is PNG, but the quality is not good yet. Do you have any ideas for a better quality? </s> | * Roozbeh to Allison: <b>Fig. 5</b>, although the format is PNG, but the quality is not good yet. Do you have any ideas for a better quality? </s> | ||
* Roozbeh to All: <b>Line ?</b>, What was this sentence at the end of the wiki? "Gossip strengthens the relationship between ego and alter and weakens an already weak relationship between the two and a third actor.". I have not added that to the paper. Please let me know if you want to include it. | * <s>Roozbeh to All: <b>Line ?</b>, What was this sentence at the end of the wiki? "Gossip strengthens the relationship between ego and alter and weakens an already weak relationship between the two and a third actor.". I have not added that to the paper. Please let me know if you want to include it.</s> | ||
* Milena: <b>authors</b>, Can we put the names and the affiliations (university only, no city necessary) in horizontal lines so that we can fit Chang's and my long e-mail addresses? Alternatively, we can add the affiliations and contact information as a footnote. | ** Milena: That's a summary of the Wittek article quoted above. Ignore it. Btw, I just realized that the class I'll be taking this semester at the University of Groningen is taught by the same Wittek!!! Any questions for him? I'll try and use this article to get to chat to him and pique his interest in our own paper... | ||
** Allison: I think the standard method is to list authors and put the affiliations as footnotes. Roozbeh can you add my middle initial (K). | * <s>Milena: <b>authors</b>, Can we put the names and the affiliations (university only, no city necessary) in horizontal lines so that we can fit Chang's and my long e-mail addresses? Alternatively, we can add the affiliations and contact information as a footnote. | ||
* Allison: <b>Line 1</b>:rewrite as "In this paper we develop a simple model for the effect" | ** Allison: I think the standard method is to list authors and put the affiliations as footnotes. Roozbeh can you add my middle initial (K).</s> | ||
* <s>Allison: <b>Line 1</b>:rewrite as "In this paper we develop a simple model for the effect" | |||
* Allison: <b>Line 5</b>: change to "weakens both B-C" | * Allison: <b>Line 5</b>: change to "weakens both B-C" | ||
* Allison: <b>Line 6</b>:change to "if gossip does not spread beyond simple triads" | * Allison: <b>Line 6</b>:change to "if gossip does not spread beyond simple triads" | ||
* Allison: <b>Line 10</b>:change to "here we show" | * Allison: <b>Line 10</b>:change to "here we show" | ||
* Milena: <b>Line 18</b>, O in GOssip should be lower case o. | * Milena: <b>Line 18</b>, O in GOssip should be lower case o. | ||
* Allison: <b>Line 25</b>: Instead of "[7]" write as "Dunbar (2004)" to start the sentence | * Allison: <b>Line 25</b>: Instead of "[7]" write as "Dunbar (2004)" to start the sentence</s> | ||
* Milena: <b>Lines 43-45</b>, I don't know the convention here but don't ''[4], [9]'' and ''[2], [12], [15], [18]'' look better as ''[4, 9]'' and ''[2, 12, 15, 18]''? | * Milena: <b>Lines 43-45</b>, I don't know the convention here but don't ''[4], [9]'' and ''[2], [12], [15], [18]'' look better as ''[4, 9]'' and ''[2, 12, 15, 18]''? | ||
** Allison: I agree | ** Allison: I agree | ||
* Milena: <b>Line 69</b>, Redundant, replace ''We built a simple network model (built in NetLogo [17])'' with ''We built a simple network model in NetLogo [17]'' | ** Roozbeh: I agree, too. I tried to integrate them, but it didn't work. I will send the LaTeX file to you and maybe you can figure it out. | ||
* Milena: <b>Line 81</b>, Add space between ''the'' and ''’originator’''. | ** Allison: It seems that there's something in the documentclass IEEEtran that prevents this | ||
* <s>Milena: <b>Line 69</b>, Redundant, replace ''We built a simple network model (built in NetLogo [17])'' with ''We built a simple network model in NetLogo [17]'' | |||
* Milena: <b>Line 81</b>, Add space between ''the'' and ''’originator’''.</s> | |||
* Milena: <b>Lines 93-100</b>, I had added two additional sentences in this part (see the text in the wiki). Feel free to add them if they make sense. | * Milena: <b>Lines 93-100</b>, I had added two additional sentences in this part (see the text in the wiki). Feel free to add them if they make sense. | ||
* Allison: <b>Line 101-102</b>change to "strength of 0.5 at the start of the simulations and those links whose weight dropped below 0.0005, during the course of the simulation, were severed." | * <s>Allison: <b>Line 101-102</b>change to "strength of 0.5 at the start of the simulations and those links whose weight dropped below 0.0005, during the course of the simulation, were severed." | ||
* Milena: <b>Line 109</b>, Add full stop at the end of the sentence. | * Milena: <b>Line 109</b>, Add full stop at the end of the sentence. | ||
* Allison: <b>Line 111</b> change to "varied with network structure: random" | * Allison: <b>Line 111</b> change to "varied with network structure: random" | ||
| Line 275: | Line 278: | ||
* Milena: <b>Line 136</b>, Add ''(see Algorithm 4)'' before the full stop. | * Milena: <b>Line 136</b>, Add ''(see Algorithm 4)'' before the full stop. | ||
* Milena: <b>Algorithm 3</b>, We don't refer to the variable names we use in the simulation elsewhere, so I would suggest that we are more descriptive in the title. Replace ''Victim-Choice = Degree-Random'' with ''Model with Popular Agents More Likely as Victim'' or something of this sort. | * Milena: <b>Algorithm 3</b>, We don't refer to the variable names we use in the simulation elsewhere, so I would suggest that we are more descriptive in the title. Replace ''Victim-Choice = Degree-Random'' with ''Model with Popular Agents More Likely as Victim'' or something of this sort. | ||
* Milena: <b>Algorithm 4</b>, Replace ''Originator-Choice = Weakest-Link'' with ''Model with Victim's Weakest Link as Originator'' or something of this sort. | * Milena: <b>Algorithm 4</b>, Replace ''Originator-Choice = Weakest-Link'' with ''Model with Victim's Weakest Link as Originator'' or something of this sort.</s> | ||
* Milena: <b>Fig.3</b>, Can we make this figure smaller and move it after Line 161? | * <s>Milena: <b>Fig.3</b>, Can we make this figure smaller and move it after Line 161?</s> | ||
* Allison: <b>Line 156</b>change the part in parentheses to "see Results" | * <s>Allison: <b>Line 156</b>change the part in parentheses to "see Results" | ||
* Milena: <b>Lines 159-160</b>, We should add that the analysis is executed for the quadratic function only. I suggest: For the simplest case, we assume that we have only three connected nodes ''and that links change according to the quadratic function''. | * Milena: <b>Lines 159-160</b>, We should add that the analysis is executed for the quadratic function only. I suggest: For the simplest case, we assume that we have only three connected nodes ''and that links change according to the quadratic function''.</s> | ||
* <b>ANALYSIS:</b> | * <b>ANALYSIS:</b> | ||
** Allison: <b>Line 162-3</b> Shouldn't this be that c->c^2, a->a^(1/2) and b->b^(1/2)? | ** <s> Allison: <b>Line 162-3</b> Shouldn't this be that c->c^2, a->a^(1/2) and b->b^(1/2)? | ||
** Allison: <b>Equation 1</b> after n steps doesn't c become c^(2^n) NOT c^(2n)=(c^2)^n? Also get a^((1/2)^n) and b^((1/2)^n) | *** Milena: I don't think so. Our link-change function assumes that <b>0 < a, b, c < 1</b> and relationship c increases, while a and b decrease. | ||
** Allison: <b>Equation 2</b> That means that for Eq2 we get a^[(1/2)^(2n/3) * 2^(n/3)]=a^[(1/2)^(n/3)] which goes to zero as n goes to infinity | ** Allison: oops, I was thinking c->c^2 increased, not decreased, sorry!</s> | ||
** <s>Allison: <b>Equation 1</b> after n steps doesn't c become c^(2^n) NOT c^(2n)=(c^2)^n? Also get a^((1/2)^n) and b^((1/2)^n) really a^(2^n), b^(2^n), and c^((1/2)^n) | |||
*** Milena: True about the powers, just reverse the letters.</s> | |||
** Allison: <b>Equation 2</b> That means that for Eq2 we get <s>a^[(1/2)^(2n/3) * 2^(n/3)]=a^[(1/2)^(n/3)]</s> which goes to zero as n goes to infinity | |||
*** Milena: a^[(1/2)^(n/3) * 2^(2n/3)]=a^[2^(n/3)] | |||
** Allison: actually this should be easy to extent to 4 and 5 node complete graphs as Milena suggests... | ** Allison: actually this should be easy to extent to 4 and 5 node complete graphs as Milena suggests... | ||
*** for four nodes, an edge decreases (n/2) of the time and increases (n/2) of the time so we get a^[(1/2)^(n/2) * 2^(n/2)]=a which means it doesn't change over time | *** for four nodes, an edge decreases (n/2) of the time and increases (n/2) of the time so we get a^[(1/2)^(n/2) * 2^(n/2)]=a which means it doesn't change over time | ||
***for five nodes, an edge decreases (2n/5) of the time and increase (3n/5) of the time so we get a^[(1/2)^(2n/5) * 2^(3n/5)]=a^[2^(n/5)], which increases as n goes to infinity | ***for five nodes, an edge decreases (2n/5) of the time and increase (3n/5) of the time so we get <s>a^[(1/2)^(2n/5) * 2^(3n/5)]=a^[2^(n/5)]</s>, which increases as n goes to infinity | ||
* Milena: <b>Line 165</b>, This is a new sentence - capitalize. | **** Milena: a^[2^(2n/5) * (1/2)^(3n/5)]=a^[2^(-n/5)], which approaches 1 as n goes to infinity | ||
* Milena: <b>Line 181</b>, ''become'' should be ''becomes''. | *** Allison: ...and for m nodes we get a^[2^(-n(m-4)/m)] which makes sense: for m<4 a decreases, for m=4 a stays the same, for m>4 a increases | ||
* Milena: <b>Equation 2</b>, Correct me if I'm wrong, but I think that in the formula ''(1/2)(n/3)'' should be ''(1/2)(3/n)'', since in Equation 1 we have c^(1/2n). Which means that the link weights tend to a^2. If you do the same kind of analysis for a complete network of 5 nodes (i.e. 10 links), the links tend to a^(2/3), i.e. they tend to increase in strength in the long run. | ** Allison: does this make sense and is it right? If so, it might make sense to add a fully connected 4-node and 5-node graphs to Figure 3 to illustrate. | ||
* <s>Milena: <b>Line 165</b>, This is a new sentence - capitalize. | |||
* Milena: <b>Line 181</b>, ''become'' should be ''becomes''.</s> | |||
* Milena: <b>Equation 2</b>, <s>Correct me if I'm wrong, but I think that in the formula ''(1/2)(n/3)'' should be ''(1/2)(3/n)'', since in Equation 1 we have c^(1/2n). Which means that the link weights tend to a^2. If you do the same kind of analysis for a complete network of 5 nodes (i.e. 10 links), the links tend to a^(2/3), i.e. they tend to increase in strength in the long run.</s> WRONG. | |||
** Since we cut links if their strength falls below 0.005, I feel that we need a different kind of analysis here (i.e. the probability that a link decreases consecutively to reach the critical value differs between triads and complete networks of 4, 5, etc. nodes (this reminds me of the concept of stochastic stability but I admit that I barely know what I'm talking about :) ). In any case, it may be too late to change this for the CSSS version of the paper but I was hoping to stimulate some thoughts for the paper's future iterations. | ** Since we cut links if their strength falls below 0.005, I feel that we need a different kind of analysis here (i.e. the probability that a link decreases consecutively to reach the critical value differs between triads and complete networks of 4, 5, etc. nodes (this reminds me of the concept of stochastic stability but I admit that I barely know what I'm talking about :) ). In any case, it may be too late to change this for the CSSS version of the paper but I was hoping to stimulate some thoughts for the paper's future iterations. | ||
* Milena: <b>Lines 201-202</b>, Remove the text ''(reducing the link strengths of the central node and increasing the strengths of links on the circle)''. Where did this circle come from?? | * <s>Milena: <b>Lines 201-202</b>, Remove the text ''(reducing the link strengths of the central node and increasing the strengths of links on the circle)''. Where did this circle come from??</s> | ||
* Milena: <b> Lines 203-217</b>, Roozbeh, I still don't understand this part. Why are you trying to relate the probability of being selected as a victim to the sum of the link weights? We never discuss or execute this algorithm? I suggest that you drop this part completely. | * <s>Milena: <b> Lines 203-217</b>, Roozbeh, I still don't understand this part. Why are you trying to relate the probability of being selected as a victim to the sum of the link weights? We never discuss or execute this algorithm? I suggest that you drop this part completely.</s> | ||
** Roozbeh: I wanted to omit this part in the first revision, but I completely forgot! (now it is omitted) | |||
* Milena: I suggest the following structure for the Analysis section: | |||
** ''A. Triads''. Revise as suggested above. | ** ''A. Triads''. Revise as suggested above. | ||
** ''B. Complete Clusters''. More or less repeat part A but for a complete network of 5 nodes. | ** ''B. Complete Clusters''. More or less repeat part A but for a complete network of 4 and 5 nodes. | ||
** ''C. Non-random Choice of Victim''. Lines 170-202. | ** ''C. Non-random Choice of Victim''. Lines 170-202. | ||
*** Although, for next versions, we have to rework this part too. We need to introduce notation. Also, the whole analysis has to be rewritten in terms of weakening an already weak relation rather than strengthening an already strong relationship (since this is the motivation behind the algorithm we use). Furthermore, at the end, you suddenly start talking about a central node and a circle?? I thought this analysis is done for triads... | *** Although, for next versions, we have to rework this part too. We need to introduce notation. Also, the whole analysis has to be rewritten in terms of weakening an already weak relation rather than strengthening an already strong relationship (since this is the motivation behind the algorithm we use). Furthermore, at the end, you suddenly start talking about a central node and a circle?? I thought this analysis is done for triads... | ||
* Milena: <b>Line 236</b>, Add missing colon/dash: ''...can have exactly the opposite effect: it...'' | * <s>Milena: <b>Line 236</b>, Add missing colon/dash: ''...can have exactly the opposite effect: it...'' | ||
* Milena: <b>Lines 250, 252</b>, Missing apostrophes. Change ''victims'' to ''victim's''. | * Milena: <b>Lines 250, 252</b>, Missing apostrophes. Change ''victims'' to ''victim's''. | ||
* Milena: <b>Lines 305-312</b>, Delete, this is in the caption to Fig. 8 | * Allison: <b>Lines 292-4</b> Change to "We made many simplifying assumptions in our model, several of which could be relaxed to make it more realistic. For example..." | ||
* Milena: <b>Table 1</b>, Roozbeh, can you fit the table in one column only? Also, I think it's better if you use the same captioning style as for the figures i.e. under the table saying ''Table 1. Linear Regressions...'' | * Milena: <b>Lines 305-312</b>, Delete, this is in the caption to Fig. 8 </s> | ||
* Milena: <b>Fig. 5</b>, Why is it after Fig. 6 and not before? Can you move it? | * <s>Milena: <b>Table 1</b>, Roozbeh, can you fit the table in one column only? Also, I think it's better if you use the same captioning style as for the figures i.e. under the table saying ''Table 1. Linear Regressions...''</s> | ||
* Milena: <b>Fig. 7</b>, Do we need it? We don't refer to it. I suggest we remove it. | ** <s>Roozbeh: Milena, I tried the table in one column first, but it didn't fit. The caption style of the table is imposed by the template. If we use another template, it might change (I don't recommend it for now, later we adjust it for the target journal).</s> | ||
* Milena: <b>Fig. 8</b>, In the caption, replace ''doesnt'' with ''does not''. | * <s>Milena: <b>Fig. 5</b>, Why is it after Fig. 6 and not before? Can you move it?</s> | ||
* Milena: <b>Line 330</b>, I suggest that we do not number the Acknowledgments section and leave it separate like the References section. | ** <s>This is also imposed by the template. If we try to move it (as far as I know), it won't seem good. I try to find a solution for this.</s> | ||
* <s>Milena: <b>Fig. 7</b>, Do we need it? We don't refer to it. I suggest we remove it. | |||
* Milena: <b>Fig. 8</b>, In the caption, replace ''doesnt'' with ''does not''.</s> | |||
* <s>Milena: <b>Line 330</b>, I suggest that we do not number the Acknowledgments section and leave it separate like the References section. | |||
** Allison: I think figure numbers should be removed completely when we submit the paper -- I just suggested adding them for the moment because it makes this sort of editing easier. | ** Allison: I think figure numbers should be removed completely when we submit the paper -- I just suggested adding them for the moment because it makes this sort of editing easier. | ||
* Milena: <b>Lines 341, 358</b>, Insert special characters in ''Barthélemy'' and ''Grönlund'' | ** Roozbeh: Are you two talking about the small numbers for each line? Or about having a separate section for the acknowledgment? | ||
* Allison: <b>Figures </b>: | ** Milena: I'm talking about changing ''VI. ACKNOWLEDGMENTS'' on <b>Line 330</b> to ''ACKNOWLEDGMENTS''</s> | ||
** I tried to make it like References, but I couldn't. We can change it for revisions (it's not a big deal, any way). | |||
* <s>Milena: <b>Lines 341, 358</b>, Insert special characters in ''Barthélemy'' and ''Grönlund''</s> | |||
* <s>Allison: <b>Figures </b>: | |||
** Allison I think these need to generally be moved around a bit to fit better -- they should be placed near the text where they are referenced, if possible. For example, Fig1 should go on the first page, Fig2 on the second page, Fig3 moved down to be in the analysis section, and the rest of the figures moved earlier to be in the results section and not clustered at the end. | ** Allison I think these need to generally be moved around a bit to fit better -- they should be placed near the text where they are referenced, if possible. For example, Fig1 should go on the first page, Fig2 on the second page, Fig3 moved down to be in the analysis section, and the rest of the figures moved earlier to be in the results section and not clustered at the end. | ||
** Allison: Figures should be renumbered in the order they appear in the manuscript (e.g 6 should become 4, 4-->5, 5-->6). | ** Allison: Figures should be renumbered in the order they appear in the manuscript (e.g 6 should become 4, 4-->5, 5-->6).</s> | ||
** Allison: Also Fig 7 is never referenced in the text | ** <s>Allison: Also Fig 7 is never referenced in the text</s> | ||
** Roozbeh: I added more force for figures to stay where they are inserted. Now it is better. In fact the figures are ordered the same as their reference. | |||
=== Extensions/Variants === | === Extensions/Variants === | ||
Latest revision as of 00:39, 3 September 2009
Abstract
THE EFFECT OF GOSSIP ON SOCIAL NETWORKS
In this project we study a simple model of the effects of gossip spread on social network structure. We define gossip as information passed between two individuals A and B about a third individual C which affects the strengths of all three relationships: it strengthens A-B and weakens B-C and A-C. We find out that if gossip occurs in simple triads, it destroys them but if gossip propagates through large dense clusters, it strengthens them. This work is novel in two respects. First, while past studies have looked at how network structure affects gossip spread, we here show how gossip spread affects network structure. And second, although there is previous theoretical work on how information or matter flowing through a network can change its structure, our contribution is to specifically model this process when the flow affects edges not necessarily along its direct path.
The latest pdf paper is available here: File:Gossip.pdf.

Paper Draft
Introduction
Gossip is ubiquitous in human groups and has even been argued to be fundamental to human society (Dunbar 2004). It usually has negative connotations: generally, no one wants to be thought of as a ‘gossip,’ and gossiping has traditionally been viewed as an indirect form of aggressiveness. However, gossip also seems to have a variety of benefits, including helping individuals learn the cultural rules of their societal group (Baumeister et al 2004). Dunbar (2004) even proposed that gossip is analogous to grooming in primates: it is essentially a tool to create and maintain relationships between individuals, with little importance given to the accuracy or quality of the actual information being passed.
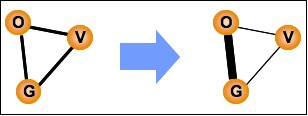
Unlike rumors, which pertain to issues and events of public concern, gossip targets the behavior and life of a private individual. Gossip can essentially be defined as information passed from one individual (originator) to another (gossiper) about an absent third individual (victim) (Lind et al. 2007). Therefore, any analysis of gossip must occur at the level of the triad or higher (Wittek & Weilers 1998). We assume, for the purpose of this paper, that gossip serves to strengthen the relationship between gossipers and weakens the relationship between the victim and each gossiper (Fig. 1).
Previous work has explored how social structure influences the flow of gossip and which network types best promote gossip (Lind et al. 2007). This work is closely related to the vast body of contagion literature (Dodds & Watts 2004) studying how cultural fads (Bikhchandani et al. 1992; Grönlund & Holme 2005), technological innovations (Abrahamson & Rosenkopf 1997) or contagious disease (Barthélemy et al. 2004; Kuperman & Abramson 2001; Morris 1993; Newman 2002) spread on networks. Gossiping, however, has the potential to change the structure of the network on which it flows by damaging some relationships while strengthening others (Wittek & Weilers 1998). This suggests a flip side to the problem of the spread of gossip that has remained unaddressed to date. In this paper, we address exactly this problem, by investigating how gossip affects the structure of the social network it flows through.
The process of an information flow molding a network has been previously studied in the context of Hebbian learning, where the simultaneous activation of neurons leads to an increase in the strength of their synaptic connection (Hebb 1949). A similar type of path reinforcement has also been observed in ants (Goss et al. 1989), humans (Helbing et al. 1997), and even slime molds (Nakagaki et al. 2000). All of the above models, however, explicitly describe modification of the network only along the flow's direct path. Information or matter passed along one network edge only affects other edges indirectly, due to a "conservation" principle: for example, because there is a finite number of ants, by choosing one path more, the ants are indirectly choosing the other paths less. Our contribution is to model how information passed along one edge can directly affect the strengths of other edges in the network.
Methods
We built a simple network model (built in NetLogo) to simulate how the spread of gossip influences social network structure. In order to guarantee convergence, each simulation was run for 10,000 gossip events. We ran simulations with 48 different parameter combinations (3 network types, 2 network sizes, 2 methods of victim choice, 2 methods of originator choice, 2 methods of changing connection strength) for 10 repetitions each, for a total of 480 simulation runs.
Model
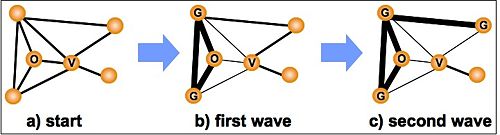
To simulate a single gossip event on a network we first choose a random node in the network to be the 'victim' of the gossip event. Then we choose one of the victim’s neighbors as the'originator' of the gossip event (Fig. 2a). In the first wave of a gossip event, the gossip is spread to all the mutual neighbors, now gossipers, of the victim and originator (Fig. 2b). In subsequent waves, each of these new gossipers then spreads the gossip to their mutual friends with the victim (Fig. 2c). This process continues until no new individuals become gossipers. (see Algorithm 1)
We assumed that spreading gossip results in a stronger relationship between all gossipers, and a weakened relationship between the victim and the gossipers. Allowing link weights to take values between 0 and 1, we used two functions describing this effect:
- normalized: For increasing, w_{n+1} \leftarrow w_n + \alpha (1-w_n) and for decreasing, w_{n+1} \leftarrow \beta w_n in which \alpha < 1 and \beta < 1. In the simulations, we fixed \alpha = 0.4 and \beta = 0.6. This method has hysteresis, i.e. an increase followed by a decrease does not necessarily lead to the initial value of strength.
- quadratic: For increasing, w_{n+1} \leftarrow sqrt{w_n} and for decreasing, w_{n+1} \leftarrow {w_n}^2. Other powers can be used for extensions. In this function, gossip has a weak effect on strong ties and a strong effect on weak ties.
All edges were initially set to have a strength of 0.5. Furthermore, those links whose weight dropped below 0.005 were severed.
Algorithm #1: Basic Model 1. for each gossip event 2: set all individuals as non-gossipers 3: choose victim: pick a random individual, chosen completely randomly 4: choose originator: pick a random neighbor of victim, chosen completely randomly 5: set originator as a gossiper 6: while there are mutual neighbors of the victim and a gossiper that are non-gossipers 7: set all mutual neighbors of the victim and each gossiper as gossipers 8: end while 9: decrease the links between the victim and each gossiper 10: increase the links between all pairs of gossipers 11: end for
To test if any results we saw were due to just strengthening and weakening connections between triads of nodes, we also ran simulations on a null-gossip network, where a single gossip event only occurred within a single triad of individuals. In other words, gossip was only allowed to spread from the originator to one other individual. (see Algorithm 2)
Algorithm #2: Null Model 1. for each gossip event 2: set all individuals as non-gossipers 3: choose victim: pick a random individual, chosen completely randomly 4: choose originator: pick a random neighbor of victim, chosen completely randomly 5: set originator as a gossiper 6: choose one random mutual neighbor of the victim and gossiper, and set as gossiper 7: decrease the links between the victim and each gossiper 8: increase the links between the pair of gossipers 9: end for
Networks
We conducted simulations on several network types to see if the effect of gossip varied with network structure. We used random, small-world, and spatially clustered networks. These network types match observed patterns of social organization and provide sufficient variation in average path length and clustering. For the small-world networks, we used the original generative algorithm (Watts & Strogatz 1998) with a rewiring probability of 0.15. The spatially clustered networks were generated by distributing the nodes randomly in space and then letting a randomly selected node establish a link with the closest node.
We also varied network size, comparing small (N=50) and large (N=200) networks with an average node degree of 6.
Alternative Gossip Algorithms
In the simplest case, the probability of becoming a gossip victim or originator is uniform across nodes. Following theoretical arguments and previous empirical findings, we also explored two additional algorithms for starting the gossip event:
- The probability to become a victim increases with degree centrality. This algorithm models the situation where more popular people are more likely to be subjects of gossip, which is the working mechanism in the hypothesis that gossip serves to equalize the social status of individuals in a network (Boehm 1999).
Algorithm #3: Victim-Choice = Degree-Random 1. for each gossip event 2: set all individuals as non-gossipers 3: choose victim: pick a random individual, chosen based on degree -- individuals with higher degree more likely to be picked 4: choose originator: pick a random neighbor of victim, chosen completely randomly 5: set originator as a gossiper 6: while there are mutual neighbors of the victim and a gossiper that are non-gossipers 7: set all mutual neighbors of the victim and each gossiper as gossipers 8: end while 9: decrease the links between the victim and each gossiper 10: increase the links between all pairs of gossipers 11: end for
- The probability to originate gossip is 1 for the agent with the weakest connection with the victim. Here, we model the expectation that one is unlikely to pass gossip about one's close friends. Indeed, it has been found that gossip tends to weaken already weak relations (Wittek & Wielers 1998).
Algorithm #4: Originator-Choice = Weakest-Link 1. for each gossip event 2: set all individuals as non-gossipers 3: choose victim: pick a random individual, chosen completely randomly 4: choose originator: pick neighbor of victim with the weakest connection to victim 5: set originator as a gossiper 6: while there are mutual neighbors of the victim and a gossiper that are non-gossipers 7: set all mutual neighbors of the victim and each gossiper as gossipers 8: end while 9: decrease the links between the victim and each gossiper 10: increase the links between all pairs of gossipers 11: end for
We discuss further examples of alternative algorithms for spreading gossip in the 'Future Directions' section below.
Statistics
To quantify the results of our simulations, we looked at the average node degree and the clustering coefficient of the network at the end of each simulation. To measure the network clustering, we first estimate the local clustering of each node (how close the node's neighbors are to being a complete graph) and then average across all nodes (Watts & Strogatz 1998).
We also looked at how final network structure, as defined by number of clusters and clustering coefficient, was related to connection strengths. We did this by including only links greater than 0.8 strength and calculating the number of clusters and clustering coefficient. Then we included links greater than 0.6 and recalculated the number of clusters and clustering coefficient. We repeated this for links greater than 0.5, 0.4 and 0.2 (see Fig. 6 and Fig. 7).
Analysis
Results
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In our model, although gossip both weakens and strengthens links, weak links break but no new links are created. Hence, a priori, we expect that gossip will decrease the network’s clustering and average node degree.
The negative effect of gossip on clustering is most extreme in the null model: when gossip does not spread but occurs randomly in triads, the simulations quickly converge to networks with zero clustering, regardless of the properties of the initial network, the link-change function or the rules for selecting a gossip victim and a gossip originator. Furthermore, triads are unstable also when gossip spreads in networks with small initial clustering. For example, the average clustering coefficient after convergence in all 160 runs with random networks is effectively zero (mean = 0.0048, std. dev. = 0.0076). These results confirm the analytical prediction that gossip breaks triads.
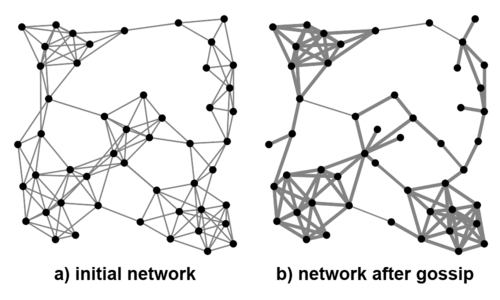
Nevertheless, in networks with sufficient initial clustering, the spread of gossip can have exactly the opposite effect – it can make certain triads more stable. When gossip originates in and spreads throughout a dense cluster, it strengthens more ties than those that it weakens. For example, in a complete network of five agents, gossip weakens only four relations (between the victim and each of the gossipers), while it strengthens six (among all gossipers). Hence, although over the long run gossip destroys weakly triangulated links (i.e. “bridges”), it makes the links in dense clusters maximally strong. The result is a more fragmented and cliquish network (Fig. 5).
When we account for initial clustering, the effect of gossip does not appear to differ among network types (Table 1). We only find that gossip tends to destroy links and weaken clustering to a lesser degree in large networks. Furthermore, when the gossip originator is the victim’s weakest link, average degree and clustering are lower compared to the case when the originator is randomly chosen from the victim’s links. This is so because, as elaborated in the analysis, under this rule weaker links become more likely to be severed.
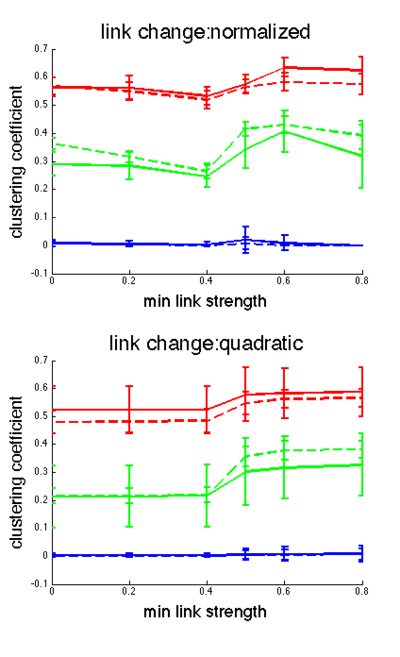
We also looked at network structure as a function of minimum link strength (only including links stronger than this 'min link strength' value for the analysis). Clustering coefficient varies little with min link strength (Fig. 6). Network type influences clustering coefficient more than network size (lines are clustered by color in Fig. 6). In contrast, the fraction of clusters varies greatly with min link strength, and seems to be influenced more by network size than network type. (Fig. 7). Random networks become especially fractured as a function of min link strength. In most cases, both metrics show the largest jump in value between 0.4 and 0.5. We believe this is due to the fact that there are likely many links in the network that are never affected by gossip over the course of the simulations, and stay at their initial 0.5 strength.
The link change rule also influences both of these network metrics. With the quadratic method, most links converge quickly to 0 or 1, leaving few links of intermediate strength. This is demonstrated by the fact that the results for the quadratic method for both methods are flat as a function of min link strength (except the discontinuity at 0.5 mentioned above). In contrast, the normalized link change method results in links that are more uniformly distributed in strength. Hence, the clustering coefficient is not flat as a function of min link strength (Fig. 6, top panel), and the fraction of possible clusters increases as a function of min link strength (Fig. 7, top panel).
Discussion / Future Directions
In this paper, we developed a general model for the effect of gossip on social structure. We only considered “negative” gossip, which we defined as an exchange of information that strengthens the relationships between those who gossip but weakens the relationships between any gossiper and the victim of gossip. We found that while gossip tends to dissolve isolated friendship triads, it strengthens them when they are embedded in dense clusters. Hence, gossip destroys clustering in weakly clustered networks and increases cliquishness in networks with already high clustering.
Many of the assumptions we made in our model are overly simplistic. Nevertheless, the model could be easily extended to be more realistic. For example, gossip does not always have to be negative. Gossip could be positive and conductive to forming new relationships (Fig. 8). Furthermore, if O shares with G positive gossip about V, G may decide to divert time from her relationship with O and start hanging out with V. This “time conservation” principle implies a potential reverse mechanism where gossip could weaken the relationship between the gossipers and strengthen the relationship between each gossiper and the gossip target. Alternatively, this very effect could also occur when somebody who has lost credibility starts maligning a third actor, i.e. when negative gossip goes wrong.

The effect of gossip could differ not only in direction but also in strength. It is reasonable to assume that the credibility of gossip decreases as you move away from its source. Consequently, a more realistic model would have the effect of gossip decreasing with each step away from the originator.
Future developments of the model should also incorporate more heterogeneity among the agents. Some individuals are more likely to originate gossip or to pass it along. People tend to exhibit conformist behavior because they pursue the fundamental sense of belonging to a group, as well as social approval from its members. Thus, being the one person in a network who doesn't gossip might lead to social isolation (McAndrew 2008). However, individuals succumb to peer pressure to different degree. Introducing individual variation in the tendency to originate or repeat gossip to the simulation model would lead to more realistic predictions about the effect of gossip on social structure.
[Do we need a concluding sentence/paragraph here? Something about the importance of the research presented here and the potential for applying it to other phenomena...?]
Acknowledgments
We would like to thank the Santa Fe Institute for giving the opportunity to work on this project via the 2009 Complex Systems Summer School. We would also like to thank Dr. Tom Carter for all his helpful comments. A.K.S. would like to thank Mark Laidre for conversations that originally inspired the project concept.
References
- Abrahamson, Eric, and Lori Rosenkopf. 1997. Social Network Effects on the Extent of Innovation Diffusion: A Computer Simulation. Organization Science 8(3):289-309.
- Barthélemy, Marc, Alain Barrat, Romualdo Pastor-Satorras, and Alessandro Vespignani. 2004. Velocity and Hierarchical Spread of Epidemic Outbreaks in Scale-Free Networks. Physical Review Letters 92, 178701.
- Baumeister, R.F., L. Zhang, and K.D. Vohs. 2004. Gossip as Cultural Learning. Review of General Psychology 8:111-121.
- not as relevant, but suggests that gossip helps individuals learn cultural rules of their group
- Bikhchandani, Sushil, David Hirshleifer, and Ivo Welch. 1992. A Theory of Fads, Fashion, Custom, and Cultural Change as Informational Cascades. Journal of Political Economy 100(5):992-1026.
- Boehm, Christopher. 1999. Hierarchy in the Forest: The Evolution of Egalitarian Behavior. Harvard University Press.
- gossip as leveling mechanism for neutralizing dominance tendency of others (cited in McAndrew 2008)
- Dodds, Peter S., and Duncan J. Watts. 2004.Universal Behavior in a Generalized Model of Contagion. Physical Review Letters 92, 218701.
- Dunbar, R.I.M. 2004. Gossip in Evolutionary Perspective. Review of General Psychology 8(2):100–110.
- Gossip is not about information but about creating and maintaining relationships (analogous to grooming among primates). Gossip also serves to control free-riders.
- Goss, S., Aron, S., Deneubourg, J. L. & Pasteels, J. M. 1989. Self-organized shortcuts in the Argentine ant. Naturwissenschaften. 76: 79-581.
- path choice in ants
- Grönlund, Andreas, and Petter Holme. 2005. A Network-Based Threshold Model for the Spreading of Fads in Society and Markets. Advances in Complex Systems 8(2/3):261-273.
- Hebb, D.O. 1949. The Organization of Behavior. New York: Wiley.
- Helbing, D., Keltsch, J. & Molnar, P. 1997. Modelling the evolution of human trail systems. Nature. 388: 47-50.
- path choice in humans
- Kuperman, Marcelo, and Guillermo Abramson. 2001. Small World Effect in an Epidemiological Model. Physical Review Letters 86, 2909 - 2912.
- Lind, Pedro G., Luciano R. da Silva, José S. Andrade Jr., and Hans J. Herrmann. 2007a. Spreading Gossip in Social Networks. Physical Review E 76, 036117.
- McAndrew, Frank T. 2008. The Science of Gossip: Why We Can't Stop Ourselves. Scientific American Mind.
- Morris, Martina. 1993. Epidemiology and Social Networks: Modeling Structured Diffusion. Sociological Methods and Research 22(1):99-126.
- Nakagaki, T., Yamada, H. & Tóth, Á. 2000. Intelligence: Maze-solving by an amoeboid organism. Nature. 407: 470.
- path choice in slime molds
- Newman, M.E.J. 2002. Spread of Epidemic Disease on Networks. Physical Review E 66, 016128.
- Watts, Duncan J., and Steven Strogatz. 1998. Collective Dynamics of 'Small-World' Networks. Nature 393(6684):440-443.
- Wittek, Rafael, and Rudi Wielers. 1998. Gossip in Organizations. Computational & Mathematical Organization Theory 4(2):189–204.
- Gossip strengthens the relationship between ego and alter and weakens an already weak relationship between the two and a third actor.
More Info / To Include
To correct in paper
Roozbeh to All: Line 0, Isn't the title too general?Milena: Naah, I think it's fine.
Roozbeh to Allison: Fig. 4, although the format is PNG, but the quality is not good yet. Do you have any ideas for a better quality?- Allison: sorry about that, I've fixed them and emailed you new ones.
Roozbeh to Allison: Fig. 5, although the format is PNG, but the quality is not good yet. Do you have any ideas for a better quality?Roozbeh to All: Line ?, What was this sentence at the end of the wiki? "Gossip strengthens the relationship between ego and alter and weakens an already weak relationship between the two and a third actor.". I have not added that to the paper. Please let me know if you want to include it.- Milena: That's a summary of the Wittek article quoted above. Ignore it. Btw, I just realized that the class I'll be taking this semester at the University of Groningen is taught by the same Wittek!!! Any questions for him? I'll try and use this article to get to chat to him and pique his interest in our own paper...
Milena: authors, Can we put the names and the affiliations (university only, no city necessary) in horizontal lines so that we can fit Chang's and my long e-mail addresses? Alternatively, we can add the affiliations and contact information as a footnote.Allison: I think the standard method is to list authors and put the affiliations as footnotes. Roozbeh can you add my middle initial (K).
Allison: Line 1:rewrite as "In this paper we develop a simple model for the effect"- Allison: Line 5: change to "weakens both B-C"
- Allison: Line 6:change to "if gossip does not spread beyond simple triads"
- Allison: Line 10:change to "here we show"
- Milena: Line 18, O in GOssip should be lower case o.
Allison: Line 25: Instead of "[7]" write as "Dunbar (2004)" to start the sentence- Milena: Lines 43-45, I don't know the convention here but don't [4], [9] and [2], [12], [15], [18] look better as [4, 9] and [2, 12, 15, 18]?
- Allison: I agree
- Roozbeh: I agree, too. I tried to integrate them, but it didn't work. I will send the LaTeX file to you and maybe you can figure it out.
- Allison: It seems that there's something in the documentclass IEEEtran that prevents this
Milena: Line 69, Redundant, replace We built a simple network model (built in NetLogo [17]) with We built a simple network model in NetLogo [17]Milena: Line 81, Add space between the and ’originator’.- Milena: Lines 93-100, I had added two additional sentences in this part (see the text in the wiki). Feel free to add them if they make sense.
Allison: Line 101-102change to "strength of 0.5 at the start of the simulations and those links whose weight dropped below 0.0005, during the course of the simulation, were severed."- Milena: Line 109, Add full stop at the end of the sentence.
- Allison: Line 111 change to "varied with network structure: random"
- Allison: Line 122 change to "networks, each with an"
- Milena: Line 130, Add (see Algorithm 3) before the full stop.
- Milena: Line 136, Add (see Algorithm 4) before the full stop.
- Milena: Algorithm 3, We don't refer to the variable names we use in the simulation elsewhere, so I would suggest that we are more descriptive in the title. Replace Victim-Choice = Degree-Random with Model with Popular Agents More Likely as Victim or something of this sort.
Milena: Algorithm 4, Replace Originator-Choice = Weakest-Link with Model with Victim's Weakest Link as Originator or something of this sort.Milena: Fig.3, Can we make this figure smaller and move it after Line 161?Allison: Line 156change the part in parentheses to "see Results"Milena: Lines 159-160, We should add that the analysis is executed for the quadratic function only. I suggest: For the simplest case, we assume that we have only three connected nodes and that links change according to the quadratic function.- ANALYSIS:
Allison: Line 162-3 Shouldn't this be that c->c^2, a->a^(1/2) and b->b^(1/2)?- Milena: I don't think so. Our link-change function assumes that 0 < a, b, c < 1 and relationship c increases, while a and b decrease.
Allison: oops, I was thinking c->c^2 increased, not decreased, sorry!Allison: Equation 1 after n steps doesn't c become c^(2^n) NOT c^(2n)=(c^2)^n? Also get a^((1/2)^n) and b^((1/2)^n) really a^(2^n), b^(2^n), and c^((1/2)^n)Milena: True about the powers, just reverse the letters.
- Allison: Equation 2 That means that for Eq2 we get
a^[(1/2)^(2n/3) * 2^(n/3)]=a^[(1/2)^(n/3)]which goes to zero as n goes to infinity- Milena: a^[(1/2)^(n/3) * 2^(2n/3)]=a^[2^(n/3)]
- Allison: actually this should be easy to extent to 4 and 5 node complete graphs as Milena suggests...
- for four nodes, an edge decreases (n/2) of the time and increases (n/2) of the time so we get a^[(1/2)^(n/2) * 2^(n/2)]=a which means it doesn't change over time
- for five nodes, an edge decreases (2n/5) of the time and increase (3n/5) of the time so we get
a^[(1/2)^(2n/5) * 2^(3n/5)]=a^[2^(n/5)], which increases as n goes to infinity- Milena: a^[2^(2n/5) * (1/2)^(3n/5)]=a^[2^(-n/5)], which approaches 1 as n goes to infinity
- Allison: ...and for m nodes we get a^[2^(-n(m-4)/m)] which makes sense: for m<4 a decreases, for m=4 a stays the same, for m>4 a increases
- Allison: does this make sense and is it right? If so, it might make sense to add a fully connected 4-node and 5-node graphs to Figure 3 to illustrate.
Milena: Line 165, This is a new sentence - capitalize.Milena: Line 181, become should be becomes.- Milena: Equation 2,
Correct me if I'm wrong, but I think that in the formula (1/2)(n/3) should be (1/2)(3/n), since in Equation 1 we have c^(1/2n). Which means that the link weights tend to a^2. If you do the same kind of analysis for a complete network of 5 nodes (i.e. 10 links), the links tend to a^(2/3), i.e. they tend to increase in strength in the long run.WRONG.- Since we cut links if their strength falls below 0.005, I feel that we need a different kind of analysis here (i.e. the probability that a link decreases consecutively to reach the critical value differs between triads and complete networks of 4, 5, etc. nodes (this reminds me of the concept of stochastic stability but I admit that I barely know what I'm talking about :) ). In any case, it may be too late to change this for the CSSS version of the paper but I was hoping to stimulate some thoughts for the paper's future iterations.
Milena: Lines 201-202, Remove the text (reducing the link strengths of the central node and increasing the strengths of links on the circle). Where did this circle come from??Milena: Lines 203-217, Roozbeh, I still don't understand this part. Why are you trying to relate the probability of being selected as a victim to the sum of the link weights? We never discuss or execute this algorithm? I suggest that you drop this part completely.- Roozbeh: I wanted to omit this part in the first revision, but I completely forgot! (now it is omitted)
- Milena: I suggest the following structure for the Analysis section:
- A. Triads. Revise as suggested above.
- B. Complete Clusters. More or less repeat part A but for a complete network of 4 and 5 nodes.
- C. Non-random Choice of Victim. Lines 170-202.
- Although, for next versions, we have to rework this part too. We need to introduce notation. Also, the whole analysis has to be rewritten in terms of weakening an already weak relation rather than strengthening an already strong relationship (since this is the motivation behind the algorithm we use). Furthermore, at the end, you suddenly start talking about a central node and a circle?? I thought this analysis is done for triads...
Milena: Line 236, Add missing colon/dash: ...can have exactly the opposite effect: it...- Milena: Lines 250, 252, Missing apostrophes. Change victims to victim's.
- Allison: Lines 292-4 Change to "We made many simplifying assumptions in our model, several of which could be relaxed to make it more realistic. For example..."
Milena: Lines 305-312, Delete, this is in the caption to Fig. 8Milena: Table 1, Roozbeh, can you fit the table in one column only? Also, I think it's better if you use the same captioning style as for the figures i.e. under the table saying Table 1. Linear Regressions...Roozbeh: Milena, I tried the table in one column first, but it didn't fit. The caption style of the table is imposed by the template. If we use another template, it might change (I don't recommend it for now, later we adjust it for the target journal).
Milena: Fig. 5, Why is it after Fig. 6 and not before? Can you move it?This is also imposed by the template. If we try to move it (as far as I know), it won't seem good. I try to find a solution for this.
Milena: Fig. 7, Do we need it? We don't refer to it. I suggest we remove it.Milena: Fig. 8, In the caption, replace doesnt with does not.Milena: Line 330, I suggest that we do not number the Acknowledgments section and leave it separate like the References section.- Allison: I think figure numbers should be removed completely when we submit the paper -- I just suggested adding them for the moment because it makes this sort of editing easier.
- Roozbeh: Are you two talking about the small numbers for each line? Or about having a separate section for the acknowledgment?
Milena: I'm talking about changing VI. ACKNOWLEDGMENTS on Line 330 to ACKNOWLEDGMENTS- I tried to make it like References, but I couldn't. We can change it for revisions (it's not a big deal, any way).
Milena: Lines 341, 358, Insert special characters in Barthélemy and GrönlundAllison: Figures :- Allison I think these need to generally be moved around a bit to fit better -- they should be placed near the text where they are referenced, if possible. For example, Fig1 should go on the first page, Fig2 on the second page, Fig3 moved down to be in the analysis section, and the rest of the figures moved earlier to be in the results section and not clustered at the end.
Allison: Figures should be renumbered in the order they appear in the manuscript (e.g 6 should become 4, 4-->5, 5-->6).Allison: Also Fig 7 is never referenced in the text- Roozbeh: I added more force for figures to stay where they are inserted. Now it is better. In fact the figures are ordered the same as their reference.
Extensions/Variants
SIMPLE:
- in model2: if A gossips to five secondary individuals (B1,B2,...) about C, does A-C increase 5x over?
ALTERNATIVE GOSSIP RULES:
- how do networks resulting from positive vs negative gossip differ?
- * (a priori expect that positive gossip will result in the network becoming more connected)
- combined gossip types: pass both positive and negative gossip through network, vary % positive
- let all links (friendships) grow over time according to some function. gossip events change link location on curve (negative moves down, positive moves up).
HETEROGENEITY:
- individual variation: tendency to gossip, gossip target, impact of gossip
- individual behavior: individuals can choose to pass on the gossip, ignore it, or reject the gossiper and sever the connection
- How do individual properties (e.g. range of social circle, poverty, wealth, the information itself, or geographic location) speed up or slow down the spread of gossip?
- Can individuals influence their location in a network (e.g. increase centrality) by changing their gossiping frequency?
- In the heterogeneity model, we add conformity behavior to nodes. Conformity behavior happens to everyone when a person pursues the fundamental sense of belongingness or social approval from groups. A person tends to follow the majority behavior in a group because he is eager to be admitted and accepted. Even it means to go against his original perceptions. Study shows that individuals with a high need for social approval will distort their judgments of objectively determinable stimuli in response to perceived group pressure more frequently(Strickland, Bonnie R.; Crowne, Douglas P.1962). In this model, the probability of a node to become an originator depends on the Tendancy_to_Originate_Gossip which is a slider in the interface.
- Also we consider how peer pressure from gossiping group pushes a node to be a gossiper. According to Solomon Asch, that social influences shape every person's practices, judgments and beliefs is a truism to which anyone will readily assent(Solomon Asch.1955). It means a node will join in the gossiping group to be a gossiper under the group pressure although he initially doesn’t want to be.
Predictions
- (ref?): gossiping leads to segmentation of a network where small well-connected clusters form. (A fully-connected network will turn into a small-world network with gossip.)
- (Boehm 1999, as cited in McAndrew 2008): gossip leads to equalization of social status of individuals in a network, using sum of all edges as proxy for social status. (A network where individuals have uneven social status will even out with gossip.)
- (McAndrew 2008): being the one person in a network who doesn't gossip will lead to social isolation
- (McAndrew 2008): being the person who always spreads gossip will lead to a reputation as untrustworthy
Relevant Literature
- Burt, Ronald S. 2001. Bandwidth and Echo: Trust, Information, and Gossip in Social Networks. In Networks and Markets, Alessandra Casella and James E. Rauch, eds. Russell Sage Foundation.
- Social dynamics at play in the spread of gossip: biases in the selection of trusted third parties (one draws a sample of information consistent with one’s predisposition), the reinforcement of opinions in dyads due to an etiquette mechanism, the exaggeration of information in triads due to echo effects.
- Lind, Pedro G., Luciano R. da Silva, José S. Andrade Jr., and Hans J. Herrmann. 2006. How Gossip Propagates.
- Lind, Pedro G., Luciano R. da Silva, José S. Andrade Jr., and Hans J. Herrmann. 2007b. The Spread of Gossip in American Schools. EPL 78(68005):1-5.
- McAndrew, Frank T. 2008. The Science of Gossip: Why We Can't Stop Ourselves. Scientific American Mind.
- Strickland, Bonnie R.; Crowne, Douglas P. 1962. Conformity under conditions of simulated group pressure as a function of the need for social approval. Journal of Social Psychology,Vol 58(1), 1962, 171-181.
- Solomon Asch. 1955.Opinions and Social Pressure.
Participation
Members
Files
- Gossip figure schematics in powerpoint
- Data for regression analyses
- Latest pdf paper: File:Gossip.pdf
Meetings
5 August 6:30pm (GMT-4)
meeting:
- Chang and David have run some more simulations which Milena has analyzed and put into the results table on the wiki
- we had a long discussion of Milena's results table -- I think we finally understand it all now!
- it doesn't seem worth discussing the results from the null model in detail since these seem to always tend towards zero
- we decided that most of the remaining work is in working on the writing and some analysis (analytical and graphical) of data, we probably won't run any more simulations
- we divvied up tasks and decided to meet next week, same day but 1/2 hour later
for next time:
- Roozbeh:
- work more on analysis section (based on that probability of choosing a Victim is proportional to the degree and that probability of choosing an Originator is proportional (or absolute?) to the weakness os the link to the victim)
keep manuscript up to date- Add analysis section to the wiki
Update the pictures of the paper using PowerPoint pictures
- Dave:
- write description of heterogeneity model
- help edit manuscript
- Chang:
- write description of heterogeneity model
- Milena:
- work on writing -- intro/methods/results
- check null model results (does it always decay to zero?)
- post/email results to all
- Allison:
write up generic algorithms- redo clustering analysis for new results
post ppt of figures on wiki
12 August 7pm (GMT-4)
meeting:
- Where's Dave?
- When the NetLogo code was updated to run multiple replicates, the output for the clustering graphs wasn't updated...this has been updated now, and we have decided to run more replicates in order to make clustering graphs (see the wiki results section for these graphs with a single replicate).
- We decided to include heterogeneity discussion in both the methods and discussion sections. Heterogeneity that we actually analyzed goes in the results, non-analyzed heterogeneity goes in the discussion.
- We decided to meet at the same time next week.
- Both Milena and Roozbeh are traveling on Aug 27th, so we will be done with the paper by Aug 26th!
for next time:
- Roozbeh:
work more on analysis section (based on that probability of choosing a Victim is proportional to the degree and that probability of choosing an Originator is proportional (or absolute?) to the weakness os the link to the victim)Check availability of uploading equations on the wiki (and contact John Paul in case needed)I have contacted John Paul and I am waiting for his reply.Add analysis section to the wiki (from previous week)This item is dependent to the previous one. Sorry that we do not have analysis section in the wiki yet!Add a reference to the Hebb ruleKeep the manuscript up to dateConverting your updates to LaTeX needs some time (this is one reason for the lag). I will eventually update the paper with all your changes.
- Dave:
- write description of heterogeneity model
- help edit manuscript
- Chang:
- run simulations
- Milena:
- work on writing -- intro/methods/results
- add more references
- Allison:
update NetLogo code and send out againredo clustering analysis for new resultsget ant trail reference
19 August 7pm (GMT-4)
meeting:
- discussed clustering plots (difference between normalized/quadratic and big jump at 0.5)
- just one more meeting next week -- same time
- Wiki will be in the most updated state by Tuesday Aug 25, 07:00 PM ET
for next time:
- everyone: help write/edit the paper by Tues evening
- Roozbeh:
- Analyze the relation between network size and total amount of change in strengths
- Analyze the relation between initial connectivity of the cluster and connectedness of it after gossip
- Remove Fig.6, Fig.7, Fig.8
- Update the final paper after Tuesday Aug 25, 07:00 PM ET
- Dave:
- ...
- Chang:
- ...
- Milena:
- ...
- Allison:
generate figures from clustering analysis (png format)write results section on these figs
26 August 7pm (GMT-4)
meeting:
- last meeting!
- paper draft is essentially done. Roozbeh will convert to pdf, email to everyone by Friday, we'll write back with last minute changes by Monday and submit to SFI.
- next step is getting feedback from people about 1) quality of work, 2) what it's lacking, and 3) where to submit to.
- we'll ask Dan Rockmore for feedback, and anyone's advisors who are interested
tasks:
- Roozbeh:
Update the manuscript and send to othersRemove Fig.6, Fig.7, Fig.8Remove the unnecessary parts of analysis
Tasks
Allison/Roozbeh: create null model in NetLogoMilena/Roozbeh: create spreading model in NetLogoMilena: create NetLogo function to build different network typesRoozbeh: come up with list of relevant network metrics and implement in NetLogodegree distribution, done!average path lengthclustering coefficientnumber of clusters, done!
- create NetLogo function to implement different gossip spreading rules
- read/gather literature
- generate predictions for model results
Roozbeh: Come up with a function for increasing and decreasing weights of connections. If the type of the function does not impact the dynamics of the network, we can keep it as simple as possible. (This part is done. Now we have two increase and decrease functions for changing the weights and we just need to use them in every code. About consistency of opposite actions (increase and decrease), I did not spend more time on it as I thought that it is not a priority now).- Chang: brainstorm how to incorporate heterogeneity into the network (implementation/predictions)
Chang Yu:some ideas :)
- follower tendency: This follower tendency happens to everyone. A person's behavior is affected by a group behavior when he wants to be admitted and accepted.And he will follow the majority behavior in this group. So when a listener(initail node) becomes to a gossiper, we can make it depend on gossiper-percentage of this node's neighbors. If a% of my neighbors are gossiping, I will be a gossiper.
- contact frequency: It's a counter in the model and can remember the frequency of linking between me and other nodes respectively.When an originator or gossiper wants to share, he doesn't tell a random or every reachable neighbor. He picks the most frequent neighbor.So do others.
- keep being a listener: meaning you just don't create or spread a gossip. I'm thinking whether this situation will affect this node's friend circle. Will it weaken his link strength or decrease the contact frequency with other nodes?
Original Discussion
It could be neat to develop a model of gossip networks. If you define gossip as information passed between 2 individuals (call them A and B) about a third party (C), then the act of gossiping has the potential to change the status/connection strength of all parties involved (e.g. maybe strength A-B, and weaken A-C and B-C bonds). Essentially passing information along a path in the network changes the value of BOTH edges in the direct pathway as well as other edges in the network. These are just preliminary ideas, but perhaps we could model how gossip tendency/frequency influences the structure of a network. Also, is it possible for individuals to influence their location in a network (e.g. increase centrality) by changing their gossiping frequency? (Although this is potentially a complicated rather than complex model idea...) Let me know what you guys think! Allison Shaw
- Milena Tsvetkova: This is a very interesting idea from sociological point of view. The effect of networks on the spread of gossip is well understood: some of the social dynamics at play include biases in the selection of trusted third parties (one draws a sample of information consistent with one’s predisposition), the reinforcement of opinions in dyads due to an etiquette mechanism, the exaggeration of information in triads due to echo effects. However, I am not aware of any studies that investigate how the spread of gossip affects network structure. My work is on the coevolution of behavior and social networks so we should talk!
- XOXO Chang Yu:Interesting! Gossip is not always bad. If we can model its spreading mechanism, it could help especially when you want to spread information unofficially. I get some inspirations from Tom’s last lecture on Friday. In the gossip network, what kind of properties of these agents can speed up or reduce information spread, the range of social circle, poverty, wealth, the information itself, or even the locations of houses in a community? I think we may model the different spreading results under different properties.
David Brooks: I agree that this concept of Gossip Networks is a generic for the analysis of several potential problems. I would like to talk to you about your intended direction and methods.
Gustavo Lacerda: sounds like some interesting dynamics, but how are you going to get data?
- Milena Tsvetkova: This article may be a good starting point for a first discussion: it suggest that gossip is a mechanism for bonding social groups. Should we try and schedule a brainstorming session?
Allison Shaw: Let's meet tomorrow (Thursday) around lunchtime (maybe 1pm after we've eaten?) to discuss this project in more depth -- anyone is welcome to join in!
Roozbeh Daneshvar: I'd like to join this team. It's good that we are doing a research with the same theme (Contagion in Networks). I can share the results from the heterogeneous network research group.
