CSSS 2009 Santa Fe-Projects & Working Groups

CSSS Santa Fe 2009 Home Surveys/Evaluations Faculty U.S. Visa Requirements Participants Schedule Readings Notes Logistics Travel Projects & Working Groups Tutorials TShirts Blog After Hours Photos Project Presentations Final Papers

Brainstorming

Disease ecology of media hype

How much and event gets covered in the news often appears to depends on how much it is already covered in the news. Often this distorts reality. For example, the number of searches for "swine flu" (a proxy for media hype), do not reflect the patterns of disease spread over the same period.

Google searches for "swine flu"

Actual number of swine flu cases over the same period

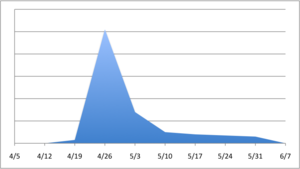
While the number of flu cases increased, the searches died off, as interest in the topic waned. It would be interesting to follow the origin, spread and extinction of media hype, maybe applying models commonly used to study the spread of disease. Alexander Mikheyev

You could look at the dynamics from agent-based (ABM) perspective. There is a recent paper by Epstein and colleague that focuses on the impact of fear on disease from agent-based perspective, but does not capture this dynamics. However, my collaborator and I are currently writing a paper on the same problem you just outline from mathematical epidemiological perspective. Our results show some interesting dynamics. I think its extension in ABM might provide richer dynamics. Another relevant paper: S. Funk, E. Gilad, C. Watkins and V.A.A Jansen (2009) the spread of awareness and its impact on epidemic outbreaks. PNAS early edition Alhaji Cherif

Housing prices.

Change in Phoenix home prices. Source: NYT

The New York Times has a set of dramatic graphs showing the rise and fall of home prices in select cities. Again these graphs reminded me a bit of those produced by susceptible-infected-recovered models of disease spread. Maybe there is something to it? Or maybe this phenomenon is already well understood by economists? Alexander Mikheyev

Movie Turnouts

Which would be the more popular movie -- a combination of Steven Spielberg, Eddie Murphy and Gwyneth Paltrow, or Woody Allen, Dwayne 'the rock' Johnson, and Tom Cruise? Using the adaptation and turnout models presented by Nathan Collins, could we construct a prediction for gross movie receipts or even movie ratings? Nathan Hodas

Climate network model.

Requires someone with climatology knowledge. Lenton et al. recently published a paper listing 'policy-relevant' 'tipping elements' in the Earth's climate system and the temperature tipping points required to initiate them. (Basically, the tipping elements are components of the climate system where a bifurcation leading to a different stable state can be induced. The tipping point is the temperature at the bifurcation.) Surely, many of these tipping elements would have feedback effects on other tipping elements or the climate system as a whole. I would like to make a network model of these tipping elements and look at the tipping (or other) dynamics of the whole system. But Lenton et al. don't discuss these feedbacks much in their model, so we need some expert knowledge. Steven Lade

Synchronised magma oscillations

Requires someone with geological knowledge In a recent paper, which was also reported by New Scientist, Mjelde and Faleide report on seismological measurements that allowed them to infer past rates of magma flow in the plume generally though to rise beneath Iceland. When the plume is strong it thickens the Earth's crust at this point. They found the crust thickened approximately every 15 million years, and inferred that the magma plume must also have pulsed with this period. These pulsations have also been observed in the crust under Hawaii, with almost exactly the same period! Mjelde and Faleide hypothesise that there must be some giant heating oscillation in the Earth's core which drives these two oscillations at very different parts of the Earth. But other geologists are skeptical because of the huge energy required and lack of other evidence of such oscillations. But all this reminds me of the synchronisation phenomenon, where coupled oscillators, even if only weakly coupled, tend to synchronise. So the oscillations under Hawaii and Iceland may be generated independently, but have some weak coupling that has led them to synchronise. We can make coupled oscillator models, that's easy, but someone to provide more context on possible forms of coupling and their parameterisation is more what we need. They only observe about three periods of this oscillation and the data is quite imprecise so we can't do much direct data analysis, unfortunately. Steven Lade

Implementing Synchronization using NetLogo

Since I just learned about NetLogo, I look forward to the tutorial sessions and would like to implement a synchronization scheme of a group of entities. If I find out how the fireflies synchronize themselves, then that would be an option. Of course, I'll be surprised if this has not been done before in NetLogo. I'll welcome any help and suggestions.Mahyar Malekpour

The Global Spread of Cricket

No I'm not actually intending to study this particular topic. But there is one interesting article published in 2005 (Kaufman and Patterson, American Sociological Review) that examined why cricket continues to be popular in many British-influenced societies while it is not in the U.S. and Canada. This is interesting given the fact that cricket was very popular in the two countries and that the first official international cricket match took place between the two countries in the mid-19th century. So, not only how cultures, ideas, technologies, etc. diffuse across nations, populations, and so on, but also mechanisms that influence the retention after the initial adoption merit serious attention I think. One possible topic include is modern contraceptive use in developing countries. I guess modeling such mechanisms would require taking into account the models presented by Nathan Collins and Peter Dodds, in addition to signed networks (Doreian). One difficulty of modeling this kind of mechanism is that both structural and individual factors should be considered Hirotoshi Yoshioka.

Contagion in Networks

Peter Dodds discussed contagion in a simplified network in which all the nodes have certain amount of threshold for changing. I thought that if the thresholds are various, that can lead to new behaviors in group level. For instance, people in different cities might have different resistances against inputs. Hence, we might see that an epidemic issue spreads in one city but not in the other. Consider the cities as nodes in a higher level network. This means that we might see the same patterns in this higher level. Different nodes (cities) react differently to external inputs. This also seems to be a more realistic model of the real world. Any comments, suggestions or discussions, even in the order of minutes are appreciated! Roozbeh Daneshvar

Perhaps this concept could be related to ecological food webs and the success of invasive species. The "epidemic" would be an introduced species, and the "spreading of the disease" would be how successful the alien species is within that food web. There are plenty of journal articles attempting to study the success of biological invasion, and I think in addition to looking at the food web networks, generating an agent based model would be ideal! It could be related to your idea, Roozbeh, in that the cities represent "habitats", and the "epidemics" represent the introduction of an alien species.

Introducing Agent-Based Modeling: Several concepts (external and internal inputs) have been discussed that are said to contribute to whether or not a species succeeds in it's novel environment. These include: how many individuals are in the founding population, the "strength" of any competing organisms (this would be 0 is there are no competitors), the amount resources available, the ability of organism to adapt to the new environment, physiological advantages of new species over native species (i.e. defense mechanisms), and many more. I think we could find properties of ecological foodwebs, and then introduce a species (or epidemic) into the network and see what happens based on these inputs.

Let me know your thoughts. Karen Simpson

Linking topology to dynamic response in small networks

Imagine a small (3-7 nodes) network where every node represents a protein species, and every (directed) edge the activation relation between the proteins (i.e. A ---> B means that the protein A can react with B and activate it). Furthermore, assume that there are two numbers associated with every node: the total number of protein molecules of the given type and the fraction of the active forms. Finally, let two nodes, R and E, be special and call them the Receptor and the Effector. What you have is a crude model of intracellular signalling.

This paper considers such models and exhaustively classifies all the possible topologies (i.e. wirings) with respect to the activation pattern of the Effector in response to a standardized signal sent by the Receptor. The goal of our project would be to do the same experiment using different tools, and potentially obtain different results. The main difference would be to use stochastic (rather than deterministic) dynamics to determine the response. As the signalling systems operate with relatively low numbers of molecules, stochastic effects may be important. If we do this and have time left, we can try pushing it further and consider the issues of robustness and evolvability of these networks.

To put a nasty spin on the project, I propose that we use an obscure computational technique called model checking to get the response profile of a network; partly just because we can, but partly also because it nicely deals away with the need of explicitely simulating and averaging of stochastic models.

Now, a couple of final remarks:

• Don't think of it as a network project. All networks involved will be rather trivial.
• The project group should include a biologist (to do sanity checks) and somebody familiar with parallel computing.
• Model checking is (very) expensive computationally, we will probably need a cluster.
• I have all the original results from the paper mentioned.
• The tool to use would probably be PRISM.

Marek Kwiatkowski

Marek, this dovetails nicely with my interests & I'd like to talk more about it with you. I have experience with -- and access to! -- a parallel cluster. No experience with prism, however. Rosemary Braun

OK then, I am going to start a From Topology to Response project page. We still need a biologist. Marek Kwiatkowski

Pattern Generation in Dynamic Networks: Elucidating Structure-to-Behavior Relationships

Many sorts of networks produce patterns when dynamics are active on them. The brain is a great example. In fact, the patterns generated in your head are not only interesting and perhaps beautiful, but crucial to your success in surviving and thriving in the world. Gene or protein networks are another example. Change a few genes around and suddenly your stuck with a nasty disease.

One question we can ask is: how do the patterns of behavior (or "function" if you want to presume as much) change when we change the structural connections in the dynamic network from which they emerge? Alternatively, for a given type of behavior (set of similar patterns), is there a class of networks which all exhibit this behavior? What is common between all of those networks? What is the underlying mechanistic explanation for how they all behave this way?

Some potential topics:

• Genetics - what patterns of proteins emerge depending on what genes are where on a genome? (maybe other questions ... I'm not a geneticist!)
• Spiking neural networks - I have a lot of experience with this.
• Kauffman-like Boolean networks
• Population biology / food webs?
• Economics?

We might even think of embedding this in some physical space. Perhaps neural nets drive the 'muscle' movements of creatures (a la the Karl Sims 'Creatures' video we saw in Olaf Sporn's lecture) or the motors of vehicles.

I have experience in Python, Java, Matlab and a few other languages and am open to working with whatever (NetLogo?). I also have experience with Information Theory, which could come in handy in digesting and analyzing the patterns.

Clearly this project could go multiple directions. Feel free to add ideas/comments here...

watson

• Jacopo Tagliabue: Premise: I don't know if it makes sense at all, and even if it fits the project. I was thinking that just not the fact that some areas are connected makes a difference, but also the way they are connected. For example, the synchronization of neurons plays a pivotal role in the proper behaviour of the brain: when some disease (such as multiple sclerosis) leads to demyelination, the signals in the axioms can no more be processed at the right speed. The upshot is progressive cognitive and physical disability. Can we use agend-base models and/or network analysis to better understand what happens (and why, for example, multiple sclerosis may evolve in four different ways)? If someone with some neuroscience background would like to talk about this (or just explain why this doesn't make sense at all),I'd be glad to learn!

Karen Simpson: This is interesting to me, especially in the case of food webs merely because that is what I am most familiar with. Within an ecological community, there are certain links that depict the dynamics within that community. If we remove a link (or change it somehow, maybe by redirecting it through another organism), the community is stressed. The community may be resilient and the underlying dynamics may shift back to equilibrium. On the other hand, it may lead to the extinction of certain organisms. One way that these links are changed is by introducing another node into the system, this node representing an introduced species. The success of this species depends largely on its position in the food web and its connecting links. My question (from an ecological perspective) is: Does introducing a non-native species result in different underlying dynamics and patterns? My intuition says yes, but it largely depends on the ability of the non-native organism to succeed in it's new environment. (See my thoughts under "Contagion in Networks" for more on this topic)

All sorts of (mostly US-centric) data

For fun, brainstorming, and sanity-checking: data.gov has tons of data collected by the US Gov't.

Problem solving and mating - are they similar?

I was intrigued by Tom's model of mating and began to wonder whether we can think of problem solving in a similar way. If we were to model problem solving, how would we do it? I'd like to think that problems and solutions are components that combine to generate an emergent property. (After a problem meets a solution--or a solution meets a problem--something new is allowed to emerge. While one instance of problem solving does not exactly create a complex system, many instances may.) That said, there are several questions/considerations to think about before/while we create a proper model of problem solving:

• What is the difference between problems and solutions anyway?
• What makes certain kinds of problems and solutions "hang out" in a cluster or neighboring clusters? Is this primarily due to path-dependence?
• When there is a difficult problem (tentatively defined as a problem for which there is no nearby solutions), how can we tell which clusters have the greatest probability of containing the solution(s)? (Can some of the network stuff we learned be of help here?)
• It is of course important to remember that a problem can have many solutions, and a solution can solve many problems, but that they may have different degrees of affinity (just like a ligand-receptor interaction in molecular biology). Also, occasionally a problem needs a combination of several solutions ("AND" as opposed to "OR").

I would love to hear your thoughts and comments, and I'm hoping that someone may actually share some of my interests in figuring out the answers to the questions above! Wendy Ham

Modularity in complex systems - why is it there and what does it do?

Evolving systems often switch from being highly modular to highly integrated, and vice versa. Why is this so and how does it happen? Wendy Ham and Roozbeh Daneshvar.

• Roozbeh Daneshvar: Today in a slide of Olaf Sporns presentation, I noticed a graph showing the relation between order/disorder and complexity. When the system becomes too much ordered or too much disordered, in both cases complexity reduces. There is somewhere in between that we have the most amount of complexity. I was thinking that the emergence of modules are also a movement towards orderliness. But, complex systems do not go beyond a limit and still keep some non-modularity. So, Wendy, we have contrasting views on modularity. But maybe we will meet somewhere in between, where we have the most amount of complexity!
  • Question: Why modularity changed in human societies? Did the behavior of complexity change?
• Steven Lade Wendy, can you give some examples for evolving systems moving from "highly modular to highly integrated"? Also Roozbeh I don't understand what you mean by "behavior of complexity". Maybe we should talk.

Evolving nanomachines

Take the evolving motors animation we saw at the end of Olaf Sporn's talk, but instead put nanoscale physics, i.e. overdamped motion with Brownian noise, into the simulation. Perhaps put some basic chemistry in too. Evolve possible designs for nanomotors! What we get may include existing biological molecular motors. Or even more crazy idea: put in the physics of quantum mechanics. Steven Lade but with credits to Lilliana!

Credit Market Simulation

Money is loaned every day on the bond and money markets between banks, corporations, and individuals. It usually works very efficiently, but, ultimately, it is driven by humans. An agent simulation could provide us with insight into what behavior patterns give rise to the booms and busts that we have been experiencing. My guess is that it boils down to how individuals estimate risk and future reward. Nathan Collins suggested a learning model for how people get habituated to reward, expecting more and more for satisfaction. However, what happens to our estimates of risk in the face of increasing rewards? When the two are out of sync, we would likely see interesting dynamics. We've come up with a few ideas for how to implement this. Nathan Hodas

• Jacopo Tagliabue: It could be interesting to embed insights on risk-seeking and risk-averse behaviour from prospect theory and behavioural economics. I am also interested in agent-based simulations of a simple economy, where agents may use different heuristics (rational decision theory, Simon's model, Kahneman and Tversky theory, etc) to decide what to do. It is often said that in the market "errors cancel each other out", leaving a optimal or quasi-optimal global outcome: but is it true? And what's the relationship between individual strategies and this dynamics?

Creative Process

This is a very preliminary attempt to analyze the creative process in order to identify how we come up with ideas.

Creation of ideas as a process of random combination of concepts and connections taking place in the subconscious. Most of these ideas are filtered before reaching the conscious. Those ideas that rise above the conscious are new to the individual, some of which may also be new to the world. We generally classify the latter ideas as creative. Furthermore, the creativity literature refers to ideas as creative only when they are immediately useful in solving some problem or condition.

The existing concepts and connections can be considered as nodes or agents. A new idea can be a combination of at least 2 concepts + a connection or two connections, or some superposition of them. The following rules obey at the subconscious level:

1. The random process is taking place all the time with a single combination at one time

2. Each idea (which is a newly created concept or connection) attempts to pass through a filter. It either passes through or it doesn’t. If it does pass through, the idea is recognized and the coupling between the concepts/connections is raised. Each increase is by a factor of 0.1 (starting from 0) of the existing coupling until it reaches a maximum of 1. If it doesn't pass through, it ceases to exist (however, it may reappear later and given a change in the characteristics of the filter, they may be allowed to pass through).

The rules that define the ideas that pass through are:

1. The database of filters (individual’s understanding of the external environment, self control, etc.) defined in terms of what concept and connection associations are allowed to pass through as well as 20% deviation in them. [Ques: How can the deviation of a concept be evaluated numerically?]

Using complexity theory:

1. Agent based modeling can be used to identify how newer ideas rise to the level of consciousness, how the filters affect them

2. The network analysis can be used to understand how the coupling affects the creation of new ideas (concepts/connections)

Murad Mithani

The Biological Evolution and Social Learning of Cooperation

Both evolutionary biologists and social scientists have convincingly shown that cooperation can emerge and persist in human society. Although the two have employed the same methods (game theory and agent-based modeling), they have proposed different mechanisms: on the one hand, biological evolution based on kin selection, group selection, the “green-beard” effect or reciprocity and on the other, socio-cultural adaptation due to social learning. The two mechanisms act on different time scales and make different assumptions on the agents’ behavior (fixed vs adaptive) and the underlying dynamics (reproduction vs imitation). I think it will be interesting to combine the two mechanisms in a single agent-based model and to explore how they relate to each other. Following standard practice, the model will consist of agents on a spatial grid or a(n evolving) network who play a game such as the Prisoner’s Dilemma or Hawk-Dove. Milena Tsvetkova

Foraging on the move

Snapshot of caribou migration.

Allison Shaw: Many animals forage in groups while moving from one location to another. This means individuals have to simultaneously balance several demands: finding the best resources, maintaining the cohesion of the group, and in some cases moving in a certain direction. Can we develop an agent-based model with a simple set of individual movement rules that would allow for all these demands to be met?

This was inspired by a piece of Planet Earth footage on caribou: go to http://dsc.discovery.com/convergence/planet-earth/video-player/video-player.html, scroll down in the video clips to "Planet Earth: Plains: Following the Caribou" and watch the dynamics at about 1:30-2:00. (If anyone has a hard copy of this segment or knows how to get one, please let me know!). In this case each individual caribou pauses to eat along the way but the group never fragments and in fact it seems to almost 'flow' through an area. My guess is that one of the physicists could provide some interesting insight on how to model this.

Daniel Wuellner: Cool idea. Most importantly: I actually brought the Planet Earth DVDs with me which I'll happily lend; maybe we can organize a viewing w/ a projector somewhere.

I think there's some swarm literature out there for ideas on rules you could extend to incorporate foraging (or any other caribouish behavior). The one I know is Flocks, herds and schools: A distributed behavioral model (this actually might be the 'original' swarm paper).

Modeling Gossip Networks

It could be neat to develop a model of gossip networks. If you define gossip as information passed between 2 individuals (call them A and B) about a third party (C), then the act of gossiping has the potential to change the status/connection strength of all parties involved (e.g. maybe strength A-B, and weaken A-C and B-C bonds). Essentially passing information along a path in the network changes the value of BOTH edges in the direct pathway as well as other edges in the network. These are just preliminary ideas, but perhaps we could model how gossip tendency/frequency influences the structure of a network. Also, is it possible for individuals to influence their location in a network (e.g. increase centrality) by changing their gossiping frequency? (Although this is potentially a complicated rather than complex model idea...) Let me know what you guys think! Allison Shaw

• Milena Tsvetkova: This is a very interesting idea from sociological point of view. The effect of networks on the spread of gossip is well understood: some of the social dynamics at play include biases in the selection of trusted third parties (one draws a sample of information consistent with one’s predisposition), the reinforcement of opinions in dyads due to an etiquette mechanism, the exaggeration of information in triads due to echo effects. However, I am not aware of any studies that investigate how the spread of gossip affects network structure. My work is on the coevolution of behavior and social networks so we should talk!

The Emergence of Meaning and the Evolution of Language

There are several attempts in the philosophical and psychological literature (see Lewis’ work on convention and Grice’s analysis of meaning) to analyze the emergence of meaning. Most accounts (it not all) make extensive use of meta-representations, that is, the ability we have to understand other people intentions and “read” the content of their mental states. There are two problems with these theories: first, they are developed in a static fashion, while it may well be the case that the emergence of meaning is the result of a continuous, adaptive process; second, they seem to be plainly false, at least if we are willing to say that people affected by autism – and thus unable to read others mind – understand and produce meaning (see this recent paper by Gluer and Pagin). Brian Skyrms and others used evolutionary game theory to evolve proto-languages, so-called “signaling games”, to understand how meaning dynamically emerges without meta-representations (it turns out that meaning can be understood as a form of equilibrium in these evolutionary dynamics). It could be interesting to further develop these insights, adding more realistic features to AB models:

• adding noise
• explore the same game in different topologies and see if the emergent behaviour depends in some way on constraints on how agents move
• see if it is possible to evolve language with a proto-grammar

These are just some preliminary considerations. Let me know what you think! Jacopo Tagliabue

Biological Pathways

Loosely defined, biological pathways are networks of molecular interactions that achieve a specific biological function. I'm interested in using the information we already have about them in the analysis of microarray data. I have a bunch of half-baked ideas; here are two.

Many hits vs. critical hits

Rosemary Braun

Microarrays assay 10^5-10^6 biological markers per sample. The most basic analysis is to ask whether each marker, individually, is disease-associated; common multi-marker approach is to sort the markers based on the magnitude of their association with disease, and then ask whether the high-scoring markers are over-represented in some pathways (biological interaction networks). By systematically performing an enrichment analysis on all known pathways, it is possible to elucidate which ones may play a role in disease. (cf GSEA.)

On the other hand, it is well known that the centrality of a molecule in the biological pathway is strongly correlated with its biological importance -- the lethality of knocking out a gene is related to its centrality (eg Jeong 2001). This finding has been used to study individual markers 'within' a given pathway to predict which ones would be the most biologically relevant (eg by ranking the markers based on centrality, (http://www.ncbi.nlm.nih.gov/pubmed/18586725 Ozgur 2008)).

One of the drawbacks of GSEA-type enrichment approaches is that they do not consider the centrality of each marker, ie, they are pathway-topology-ignorant. To the best of my knowledge, while centrality has been looked at to examine the importance of individual genes to a given function, it has not been incorporated in enrichment analyses. I would like to answer the question "is a pathway more critically hit with disease-associate alterations than would be expected by chance alone" using a centrality-aware scoring function.

One very naive way to do this would be to simply scale the single-marker association statistic used in GSEA by the centrality of the gene in the network. This raises a question of its own, however: to what degree do the results depend on the severity of the scaling?

Anyway, that's one half-baked idea. [Resources available: tons of data; adjacency matrices for pathways represented in KEGG, BioCarta, Reactome, and the NCI/Nature pathway database; useful ancillary functions in R; a cluster for permutation testing/exploring the parameter space.]

Gene expression time-course spectra

Rosemary Braun

Consider all the genes involved in a given pathway. Consider, also, a set of data that gives us the expression values for each gene at a handful of timepoints, eg, before (t=t0) and after (t=tf) an environmental exposure.

Next, suppose we describe the activity of that pathway by completely connected directed graph, for which the weight of the edge from gene_i to gene_j is given by MI(gene_i(t=t0),gene_j(t=tf)) (in the case of multiple timepoints, we could extend this -- eg transfer enropy). That is, the weight of each directed edge from gene_i to gene_j would tell us how well gene_i at t=t0 predicts gene_j at t=tf.

(I suggest the complete graph, rather than using the known pathway topology, because in practice the time differences tf-t0 may result in multiple "hops" -- so we may have correlations between next-next-neighbors rather than nearest neighbors, etc.)

So, we now have a description of signal propagation through the pathway over the time t0->tf, which we could summarize using the eigenvectors of the Laplacian. If we have two classes, eg cells which do/don't respond to the exposure, will we see statistically significant differences in the spectra for certain pathways, and thus infer that those pathways are involved in the response?

Possible pitfall: most time-course experiments only have a handful of samples for each timepoint.

Interacting distribution networks

Daniel Wuellner