Foraging on the move: Difference between revisions
From Santa Fe Institute Events Wiki
| Line 259: | Line 259: | ||
** repetitions: 2 | ** repetitions: 2 | ||
** max_gen: 500 | ** max_gen: 500 | ||
** output_file: [[File:]] | |||
** plot :[[Image:july_22.jpg]] | ** plot: [[Image:july_22.jpg]] | ||
| Line 268: | Line 268: | ||
** repetitions: 2 | ** repetitions: 2 | ||
** max_gen: 1000 | ** max_gen: 1000 | ||
** output_file: | |||
** plot:[[Image:july_27.jpg]] | ** plot:[[Image:july_27.jpg]] | ||
Revision as of 00:58, 10 August 2009
Abstract
Many animals (e.g. caribou, wildebeest) forage in groups while moving from one location to another. This means individuals have to simultaneously balance several demands: finding the best resources, maintaining the cohesion of the group, and migration in a certain direction. While there is a vast literature on both flocking and optimal foraging, there has been no work done to understand how animals should trade off the decision to flock or forage (since it is difficult to do both simultaneously) during migration. We develop an individual-based model to address this, and implement a genetic algorithm to find the best decision-rule for switching between foraging and flocking, under a variety of conditions.
Project Description
Background
GROUP LIVING: Animal groups are ubiquitous in nature and their formation comes with both costs and benefits. Groups provide individuals with a lower per-capita predation rate (dilution effect), shared information, and allow individuals to find both mates and resources more easily. However, groups tend to attract predators more easily than solitary individuals, can increase the transmission rate of diseases, and lead to competition for resources. In theory the size of an animal group should be determined by the payoff to an individual; at equilibrium group size, the benefit to an individual of joining a group should be equal to that of being a loner. An individual's specific position within a group can have significant fitness consequences (see Krause 1994); individuals in the center of the group are often the safest from predation (Hamilton 1971), but those on the edge are in the best position to discover and exploit new food resources [ref].
FLOCKING & FORAGING: There is a vast literature on flocking/swarming models (e.g. [refs]), and on optimal foraging behavior (e.g. Fretwell & Lucas 1969, Schoener 1971, Charnov 1976). Some theoretical work has been done on combining foraging and flocking, but this mostly relates to what has been termed "social foraging" (see Giraldeau & Caraco 2000) and examines how how individuals can gain information about foraging locations by flocking (e.g. Clark & Mangel 1984) or on how foraging strategy should vary with respect to location within the flock (Barta et al 1997). However there is no theoretical work on how foraging individuals should behave when they are in a group that is collectively moving, a behavior seen in wildebeest, caribou and many other species of migratory ungulates. Individuals in this situation face a trade-off between foraging and keeping up with the group. Individuals that fail to forage will starve, and those that fail to keep up with the group will likely be picked off by predators [ref]. This leads to a a mixed behavior at any moment, where some individuals are concentrating on foraging and others on flocking and moving towards their destination (e.g. Planet Earth video).
MAMMALIAN MIGRATION: A recent literature review found that the majority of papers that model migration focus on birds and fish, with almost no work done on modeling mammal migration (Bauer et al 2009). The only two papers from this review that modeled terrestrial mammal migration are:
- Bergman et al (1999) found that correlated random walk model overpredicted long-range displacement of migrating caribou.
- Boone et al (2006) found that migratory pathways of wildebeest derived using an evolutionary algorithm closely matched actual migration paths chosen, suggesting that rainfall and vegetation are key determinants in wildebeest migratory behavior.
WILDEBEEST: Wildebeest in Tanzania and Kenya move in a roughly circular clockwise direction, likely following the vegetation and rainfall across the seasons. During the dry season (May-Oct), they are found mostly in the north, and move southward as the rains start, and give birth synchronously in Feb/Mar. There is a rainfall gradient (and corresponding vegetation gradient) across the region with high rainfall in the northwest and low in the southeast. (Boone et al 2006)
CARIBOU: The search for food is one of the primary drivers of caribou migration. Caribou winter in areas with a large amount of vegatation biomass (mostly lichens). In the spring they move north towards areas with seasonal vegetation that is rich in nitrogen and minerals (necessarily for rapid growth and milk production), where they give birth. In Aug/Sept as the vegetation gradient becomes less pronounced, the herds disperse in small groups, coming back together only at the end of the growing season, to migrate back south, as lichens in the wintering area become the best source of energy again. (Fancy et al 1989)
Fancy and White (1987) found that caribou were the most efficient walkers (lowest net cost of locomotion) of all ungulates tested. Wildebeest were second most efficient, suggesting that migration is an important selective pressure on locomotion efficiency.
Parameter Settings from Literature
MIGRATION RATES/DISTANCES:
- caribou migrate up to 40km/day (Fancy et al 1989)
- caribou have longest terrestrial animal migration: 1200km (Akesson 2007)
- mean migratory movement for caribou 14-26 km/day (Murray 1991)
- wildebeest migration is ~200km (Akesson 2007)
- The speed at which animal migrations can travel is dependent on three factors: speed of locomotion, rate of energy acquisition, rate of energy consumption (Akesson 2007)
- migration range shows diminishing return function with more fuel runners pay cost of extra weight (Akesson 2007)
- caribou migration rate 10-20km/day (Gunn et al 1991)
- caribou migration distance 300 to 500 km (Gunn et al. 1991)
ENERGY EXPENDITURE:
- energy cost for uphill locomotion in caribou (note: doesn't include cost of walking in snow): 22.6 (1.3 SE) kJ/(kg*m) (Fancy & White 1987)
- energy cost for horizontal caribou locomotion in snow: 1.696 KJ/(Kg*km) (Johnson et al. 2002)
- energy cost for wildebest: 4.23 kg/(individual *day) (Sinclair 1975)
- caribou are ~272kg (http://www.amnh.org/nationalcenter/Endangered/caribou/caribou.html)
- caribou are ~2m long (Kuzyk et al 1999)
- CALCULATION: (1.696kJ/kg/km)*(1km/1000m)*(272kg/ind)*(2m/body)= 0.922kJ/ind/body
ENERGY INTAKE:
- maximum consumption rate for wildebeest: 4 kg/day (Note: simulation parameter not measured) (Fryxell et al. 1988)
- energy from foraging: 169.1 KJ/(kg*day) (Murray 1991)
- 0.3 g per bite for wildebeest (Murray 1991; Figure 3/4)
- ~7.96 MJ/kg dried matter for plants (Murray 1991; Table 1)
- CALCULATION: (0.3g/bite)*(1kg/1000g)*(7.96MJ/kg)*(1000kJ/MJ) = 2.388 kJ/bite
HERD SIZE and DENSITY
- Elk winter herd size (max,min): (14,253) (Creel and Winnie 2005)
- Elk density: 13.7 individuals/ km^2 (Creel and Winnie 2005)
- Elk distance apart with in herd: <5 body lengths (Creel and Winnie 2005)
- Wildebeest main herd size in Serengeti: 467 individuals (Fryxell et al. 1988)
- Herd size in 1960 of Caribou in Newfoundland: 450 individuals (Mahoney and Schafer 2002)
- Herd size in 2000 of Caribou in Newfoundland: 6,102 individuals (Mahoney and Schafer 2002)
- Herd size in 1992 of West Arctic Caribou Herd: 417,000 (Gunn et al 1991)
MORTALITY
Methods
'NETLOGO MODEL
We created a NetLogo model to understand the balance of flocking and foraging behaviors in animal groups as they migrate. The base of our model was the NetLogo demo model (Wilensky 1998) which is based on Craig Reynolds Boids simulation (Reynolds 1987). The boids model assumes that an agent within a group moves based on two main rules. If there are other agents within a minimum separation distance radius, then the agent will turn to move away from these agents ('separate'). If there are no agents within the first radius, then the agent will align with ('align') and move towards ('cohere') any individuals within a second, larger radius ('vision'). To simulate migration, where animals are moving together in a specific direction, we add another movement rule: after agents separate, align and cohere, they also all turn towards 'north' (positive y-direction).
[create diagram of flocking rules?]'
We modified this basic flocking model by also including a foraging aspect. All agents in our model have an energy level that decreases as they spend energy moving, and increases as they acquire energy from foraging while stopped. At each time-step, every agent has to make a decision whether to forage or to flock. (Since animals such as caribou forage with their heads down, making it hard to see fellow herd-mates, we assume that it is impossible to forage and flock simultaneously.) We assume that agents make the decision of whether to flock or forage based on a simple threshold: if an agent's energy level is below a certain threshold (ForageT) it will start to forage, and if the number of agents within an agent's vision radius falls below a certain threshold (FlockT), it will start to flock. In the case where an agent is below both thresholds, we assume that flocking overrides foraging. If an agent decides to forage, it stops and increases its energy level by E_forage. If an agent decides to flock it follows the movement rules described above (separate, align, cohere, and move north), takes a step forward, and decreases its energy level by E_move. Agents can die in two ways, essentially from doing a poor job foraging or flocking. If an agent's energy level falls below a certain threshold, it 'starves' and dies. Agents have some probability of dying from 'predation', which is a function of the number of other agents it can see.
[create diagram of death by flocking and foraging: explain flocking-die-lambda, full-energy parameters]
SELECTION
We implemented a genetic algorithm type method to determine the optimal threshold values for agents. For a single run, N agents are created, each with a set of ForageT and FlockT threshold values drawn from a random distribution. The simulation is run for a single generation (which ends whenever either 20% of individuals die or 150 time-steps pass, whichever comes first). At the end of a generation, N new agents are created and the simulation is restarted. Each of these N agents gets its ForageT and FlockT threshold values from a single 'parent' -- one of the surviving agents (those that have not died from either starvation or predation) from the previous generation. These threshold values are inherited with a slight mutation rate (3% each). This process is repeated for 100 generations.
MORE:
- look at effects of population size and ratio of energy from foraging to energy spent moving* group metrics -- how does adding foraging behavior compare to just flocking?
- how are stopping time / group size / migration rate interrelated?
- do we get different movement patterns under different parameter settings -- e.g. stringy 'wildebeest' movement vs 'flowing' caribou movement?
- build in interaction with the environment (local depletion of resources)
- look at how habitat structure affects group movement
Results/Observations/Predictions
OBSERVATIONS:
- FlockingForaging_evolve_v2: continuous replacement means that population that isn't stable can be maintained by new individuals coming in
- FlockingForaging_evolve_v3: agents stay mostly sedentary
- this is fixed by changing the starting density of the simulation
- FlockingForaging_evolve_v4.nlogo: agents evolve bimodal distribution in flocking parameter
- this seems to go away when flocking takes priority over foraging (instead of the reverse)
- FlockingForaging_evolve_v4.nlogo: with mutation agents are evolving threshold for flocking larger than flock size (!) -- not sure why these are staying around since they should be unfit...
CHECK FOR (PREDICTIONS):
- Past theoretical work suggests that fragmentation of a herd results more easily for a individuals are heterogeneous in their walking speeds (Gueron et al 1993)
- Individual position within the group should change over time, as individuals change their preference for different group locations as their conditions (e.g. energy reserves) change (Parrish 1999)
- Gueron et al (1996) found that the geometry of the group was dependent on the average speed of individuals, showing bands at slow speeds and columns at fast speeds
- if cost of moving is too high, migration should 'fail'
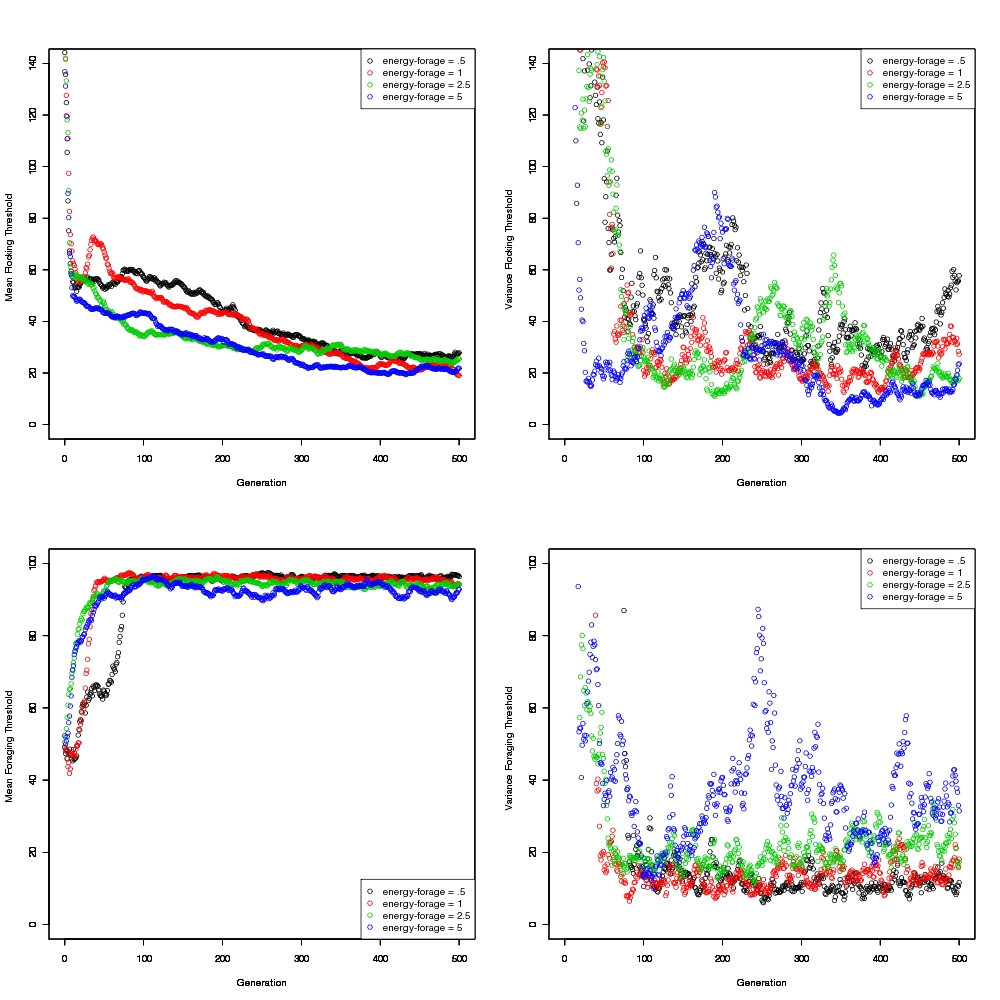
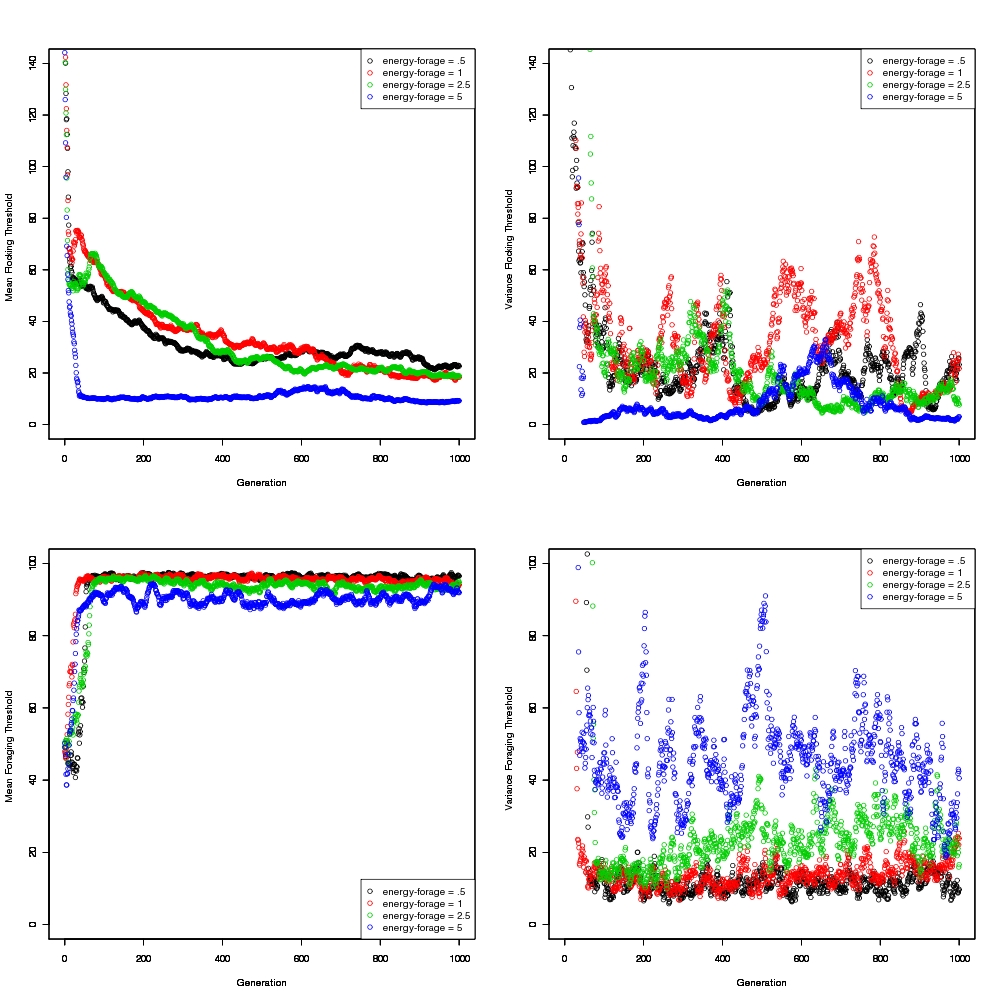
PLOTS: Here are the results from our early July simulations (10 replicates for each combination of energy and population size) ... not particularly interesting, but good for reference


References
- Åkesson, S. & Hedenström, A. 2007. How migrants get there: migratory performance and orientation. BioScience, 57, 123-133.
- Barta, Z. 1997. Geometry for a selfish foraging group: a genetic algorithm approach. Proceedings of the Royal Society B: Biological Sciences, 264, 1233-1238.
- Bauer, S., Barta, Z., Ens, B., Hays, G., Mcnamara, J. & Klaassen, M. 2009. Animal migration: linking models and data beyond taxonomic limits. Biology Letters, 1-4.
- Bergman, C., Schaefer, J. & Luttich, S. 2000. Caribou movement as a correlated random walk. Oecologia, 123, 364-374.
- Boone, R., Thirgood, S. & Hopcraft, J. 2006. Serengeti wildebeest migratory patterns modeled from rainfall and new vegetation growth. Ecology, 87, 1987-1994.
- Charnov, E. 1976. Optimal foraging, the marginal value theorem. Theoretical Population Biology, 9, 129-136.
- Clark, C. & Mangel, M. 1984. Foraging and flocking strategies: information in an uncertain environment. American Naturalist, 626-641.
- Creel, S. & Winnie, J.A. Responses of elk herd size to fine-scale spatial and temporal variation in the risk of predation by wolves. Animal Behaviour 69, 1181-1189(2005).
- de Knegt, H.J. et al. Patch density determines movement patterns and foraging efficiency of large herbivores. Behavioral Ecology (2007).
- Fancy, S. & White, R. 1987. Energy expenditures for locomotion by barren-ground caribou. Revue canadienne de zoologie, 65, 122-128.
- Fancy, S., Pank, L., Whitten, K. & Regelin, W. 1989. Seasonal movements of caribou in arctic Alaska as determined by satellite. Canadian Journal of Zoology, 67, 644-650.
- Focardi, S. & Pecchioli, E. Social cohesion and foraging decrease with group size in fallow deer (Dama dama). Behavioral Ecology and Sociobiology 59, 84-91(2005).
- Focardi, S., Marcellini, P. & Montanaro, P. Do ungulates exhibit a food density threshold? A field study of optimal foraging and movement patterns. Journal of Animal Ecology 606-620(1996).
- Frair, J.L. et al. Scales of movement by elk (Cervus elaphus) in response to heterogeneity in forage resources and predation risk. Landscape Ecology 20, 273-287(2005).
- Fretwell, S. & Lucas, H. 1969. On territorial behavior and other factors influencing habitat distribution in birds. Acta Biotheor, 19, 16-36.
- Fryxell, J.M. et al. Landscape scale, heterogeneity, and the viability of Serengeti grazers. Ecology Letters 8, 328-335(2005).
- Fryxell, J.M. et al. Why are migratory ungulates so abundant?. American Naturalist 131, 781-798(1988).
- Giraldeau, Luc-Alain and Thomas Caraco. Social foraging theory. Princeton: Princeton University Press, 2000.
- Gueron, S., Levin, S. A. & Rubenstein, D. I. 1996. The Dynamics of Herds: From Individuals to Aggregations. Journal of Theoretical Biology, 182, 85-98.
- Hamilton, W. 1971. Geometry for the selfish herd. Journal of Theoretical Biology, 31, 295-311.
- Johnson, C.J. et al. Movement parameters of ungulates and scale-specific responses to the environment. Journal of Animal Ecology 225-235(2002).
- Krause, J. 1994. Differential Fitness Returns in Relation to Spatial Position on Groups. Biological Reviews, 69, 187-206.
- Parrish, J. 1999. Complexity, Pattern, and Evolutionary Trade-Offs in Animal Aggregation. Science, 284, 99-101.
- Mueller, T. et al. In search of forage: predicting dynamic habitats of Mongolian gazelles using satellite-based estimates of vegetation productivity. Journal of Applied Ecology 45, 649-658(2008).
- Murray, M.G. Maximizing Energy Retention in Grazing Ruminants. Journal of Animal Ecology 60, 1029-1045(1991).
- Reynolds, Craig W. 1987. "Flocks, herds and schools: A distributed behavioral model." Proceedings of the 14th annual conference on Computer graphics and interactive techniques. 21: 25-34.
- Schoener, T. 1971. Theory of feeding strategies. Annual Review Of Ecology And Systematics, 2, 369-404.
- Sinclair, A.R.E. The Resource Limitation of Trophic Levels in Tropical Grassland Ecosystems. Journal of Animal Ecology 44, 497-520(1975).
- Wilensky, U. 1998. NetLogo Flocking model. http://ccl.northwestern.edu/netlogo/models/Flocking. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.
- Couzin, I. D., Krause, J., Franks, N. & Levin, S. A. (2005). Effective leadership and decision-making in animal groups on the move. Nature, 433, 513-516.
- 3-radius flocking model where individual movement is a weighted combination of the direction they inherently want to go and the influence of individuals around them
- Holdo, Ricardo M., Robert D. Holt and John M. Fryxell. (2009). "Opposing Rainfall and Plant Nutritional Gradients Best Explain the Wildebeest Migration in the Serengeti." American Naturalist. 173: 431-445.
- wildebeest migration clearly driven by rainfall gradient
- model suggests that wildebeest are maximizing green grass intake (rate of intake of high-quality food)
- video of caribou migration
Participation
Meetings
14 July 2009 7pm (GMT-4)
since last time:
- Liliana has a computer scoped out and NetLogo downloaded
- Kate added some parameters from the literature
meeting:
- got everyone connected and set up with Skype!
- divvyed tasks: Liliana and Kate will do B&F, Allison will do A, everyone will try D (we'll see who can get it to work)
- Kate suggested we reconsider how we initially setup our threshold distributions. Since we're using relatively few (N~300) agents to sample such a large distribution (0,100) by (0,100), chances are we aren't covering it uniformly. Also the different initial conditions between runs could account for different outcomes. Potential fixes: 1) increase number of individuals (thousands), 2) discretize the threshold distribution to 0-10-20-30-40 instead of continuous on (0,100).
21 July 2009 7pm (GMT-4)
since last time:
- Allison and I started to run a simulation with the following parameters: (Allison do you remember these? For some reason my netlogo file does not open anymore and I don't remember exactly which were the parameter values). I had to download the v6 version.
meeting:
- Main topic: discussion about parameter values.
- The previous simulation was taking too long (at least 21 days to run completely), so we aborted it and started a new one, where we changed the following parameters:
- population size: 300 (Kate found out from literature that population size varies a lot from herd to herd -- see parameters)
- max_gen: 500
- number of repetitions: 2
28 July 2009 7pm (GMT-4)
since last time:
Two simulations:
- 22 July:
- population: 300
- energy-forage: [0.5 1 2.5 5]
- repetitions: 2
- max_gen: 500
- 27 July:
- population: 300
- energy-forage: [0.5 1 2.5 5]
- repetitions: 2
- max_gen: 1000
meeting:
- Discussion and analysis of the data generated by the previous simulations. From a first impression it seems that with a longer run there is a higher convergence (check this out!). In the first simulation, the variance was MUCH higher than the mean (weird!)
- Next simulation: fixing the energy-threshold to 2.5 to check if the mean and variance values change.
- population: 300
- energy-forage: 2.5
- repetitions: 1-10
- max_gen: 1000
4 August 2009 7pm (GMT-4)
since last time:
The simulations with the parameters above are still running... probably will take more 3 days to finish. I learned from Allison that if we want to do repetitions, we have to write them explicitly, example for 5 repetitions: 'repetitions [1 2 3 4 5]'.
meeting:
- Analysis of the plots from the previous simulations:
- It doesn't look like increasing the number of generations changes convergence
- (still haven't checked if changing ticks/gen changes convergence)
- The foraging and flocking thresholds are both converging after 100/200 hundred generations, however, the variance doesn't seem to decrease with time. Maybe the individuals are not being selected well...
- Discussion of a new fitness measure for reproduction -- at the end of each generation, all individuals reproduce in proportion to their fitness value (ghosts are automatically), instead of the current method where all survivors (non-ghosts) have equal chance of reproducing. We thought of 2 possible fitness measures:
- An individual's fitness is just their total energy at the end of a generation. This is semi biologically realistic since individuals would be reproducing after migration and reproduction success is probably related to energy levels.
- An individual's fitness is some combination of how well they foraged and flocked throughout the simulation. This is maybe less biologically realistic, but it does reward individuals that do both activities well, which is what we're interested in.
- One possible measure for this second value could be: (Nbar/max(Nbar) + Ebar/max(Ebar)), where
- Nbar: average of the number of neighbors at each time step for an individual
- max(Nbar): maximum value of Nbar across all individuals
- Ebar: average of the the energy values at each time step for an individual
- max(Ebar): maximum value of Ebar across all individuals
- Note that we would presumably not want to average across all ticks for a generation, but have some sort of burn-in period (e.g. take the last 100 ticks of a 200 tick generation?)
- One possible measure for this second value could be: (Nbar/max(Nbar) + Ebar/max(Ebar)), where
- Implement the new fitness measure. From a first impression it seems it will be quite computational expensive to compute the averages above at each time step...
- Set up more computers with netlogo to run more simulations at the same time (Allison will check with Iain about using lab computers).
- Run new simulations with the current parameter values (check the values in the previous meeting post) but with the new fitness measure.
- Run new simulations with new group size values.
- Upload the output files (excel) from the simulations on the wiki -- Liliana
- Upload the matlab code to process NetLogo output -- Andrew
- Write a draft of the report for next meeting (only two more meetings before the deadline!)
- currently running the following on Couzin lab computer (to start checking ticks/gen effect):
- N = 300
- energy-forage = 2.5
- gen-end-time = 300
- 1000 generations
- 5 reps
11 August 2009 7pm (GMT-4)
since last time:
meeting:
Simulations
Here is a list of the different simulations that have being done. Please post the date of simulation, parameteres, output files and data analysis plots.
- 22 July:
- 27 July:
Tasks (Current)
BIG PICTURE:
- setup a base ABM of flocking and foraging (done, yay!)
- see which foraging and flocking thresholds evolve
- make sure these thresholds are 'stable' under realistic conditions for caribou/wildebeest
- see how these thresholds vary with key model parameters (population size, energy from forage, predation)
- incorporate landscape
- TASK A: Since #1 is basically done above, we should write up a clear description of the model, explaining all the parameters and logic behind them, before we forget it all!!
- I posted a first draft of the model description -- please edit if you can make it more clear or have anything to add! Might also be good to add some figures. Akshaw 14:28, 17 July 2009 (UTC)
- TASK B: try varying ticks per generation and number of generations per run (ideally on a computer cluster to avoid killing someones laptop), to see if we get tighter convergence if we run long enough
- TASK C: If B doesn't produce good results, then come up with a better metric AND figure out how to export this from NetLogo (It may just make sense to export the threshold parameter values for all individuals and not just the average/stdev)
- TASK D: Related to this, it would be good to come up with an efficient way of analyzing the NetLogo data in another program. I'm partial to MATLAB but would be absolutely ok using another program if we think that would be easier. Kate and I figured out that if you delete the header lines and replace all the quotes with commas, then the csv files are easily imported into MATLAB. However some of the data imports in as text instead of numbers. The other annoying thing is that all the stats are calculated at every tick instead of every generation. It would be great if there were someway to get just stats at every generation...
- NetLogo code modified to output data from end of generations. Also to output data in CSV format for easy import into MATLAB. Still need to modify MATLAB scripts to actually analyse the data. SteveLade 03:50, 15 July 2009 (UTC)
- TASK E: We should play around with comparing the continuous vs discrete methods. This would probably just involve running a few simulations with each to make sure we're getting similar results. It may be that things evolve faster in continuous time, so that may be the way to go for our mass simulations. There's an output graph that shows the age distribution of turtles in the population, so that you can check to make sure individuals aren't dying each tick.
- TASK F: For #3 I think we basically need to know 1) average herd size, 2) average distance/speed and 3) average mortality for caribou/wildebeest migrations. Then we can setup a population of this size and our evolved parameters and see if it can make it that distance with that mortality.
- TASK G: Related to #3 -- we should think about the form of our predation mortality term and determine the best value for sigma in the function (or perhaps use a different function). It seems that there were lots of individuals dying from flocking in the simulations.
- TASK H: Once we do at least B/C/D above, we should run simulations again varying they key model parameters that we're interested in (for #4). In the meantime though, someone could run simulations with different values to get a feel for how these change the model -- perhaps they don't change the mean population value of the thresholds but do affect the distribution, or maybe they just affect migration speed, etc.
- TASK I: Figure out exactly what we want to know by incorporating landscape/resources into the model. Do we want to add resource factors as more key parameters in the model to vary -- then see how thresholds vary under different resource distributions? If so, what would key resource parameters be? Or do we just want to see how a group would move differently across different landscape types? This would be simpler but gets away from our central question.
Tasks (Old)
LITERATURE
migration models lit review (Allison)basic description of wildebeest & caribou migration cycles (Allison)appropriate foraging parameters / energy function for ungulates: "energy-forage" and "energy-move" in NetLogo model, also probability of forage as a function of energy (Liliana)- appropriate flocking parameters / flocking lit review: "minimum-separation", "max-align-turn", "max-cohere-turn", "max-separate-turn", and "vision" in NetLogo model (Kate)
- collective behavior lit review (Allison)
- foraging lit review (Liliana)
- look for flocking metrics -- e.g. group 'coherence' or group structure/dynamics
MODEL TWEAKING (SIMPLE)
- how to initially distribute agents?
- currently are all started in roughly same area and orientation
- alternative would be to give them all the same preferred direction (a la Couzin et al 2005)
how to step model forward (appropriate time step)? ("stepsize" and "steprepeats" in NetLogo model)Have just stepsize = 1 and steprepeats (which was only smoothing) now removed SteveLade 04:59, 25 June 2009 (UTC)
problem: why do agents die from bad-foraging but do not die from bad-flocking? (or have we just not found those parameter settings?)- note: starvation rate depends on relative values of "energy-forage" and "energy-move"
- maybe have agents die from bad-flocking when too few individuals in their sight radius (instead of none)
Your sigmoidal forage-probability curve has threshold at 0.5 energy units. If energy-move is large compared to this value (and you currently have it at 0.3 by default), it will take only a couple of steps to go from 'stomach full' to 'dead'. Why there are no flocking deaths I don't know. SteveLade 04:17, 24 June 2009 (UTC)
how to prevent flock from wrapping around across the boundary?Currently not a problem -- flock not long enough
- should we stick with 2-zone model or change to 3-zone one (a la Couzin et al 2005)?
NOTE: energy levels become synchronized over time and move like a wave through the population- only happens for high "vision" values
- depends on "energy-move" values
- Doesn't seem to happen any more SteveLade 04:59, 25 June 2009 (UTC)
yeah, this was a due to a bug in how I sent initial conditions -Allison
MODEL DEVELOPMENT (MORE INVOLVED)
- develop/implement metrics to describe group
- flock density
average flock speed (Done SteveLade 04:59, 25 June 2009 (UTC))average fraction of time individual spends foraging (This is just from the ratio of energies received/spent from flocking/foraging SteveLade 04:59, 25 June 2009 (UTC))- group size stability threshold (below which group fails to flock/survive)
- group 'coherence' (check literature)
- group structure/dynamics (check lit)
adaptive dynamics framework to evolve parameters (Andrew & Steve)design behavior rules to determine when to forage and when to flock (Steve & Andrew)
- should decision to forage be independent at each time step or are foraging individuals more likely to keep foraging than to start flocking?
- Have behaviour rules but currently no hysteresis for foraging SteveLade 04:59, 25 June 2009 (UTC)
- couple foraging to changes in resource distribution -- e.g. a patch is depleted by a foraging agent and must grow back after some time
- design different landscape resource distributions to have agents moving across
Members
Original Discussion

Allison Shaw: Many animals forage in groups while moving from one location to another. This means individuals have to simultaneously balance several demands: finding the best resources, maintaining the cohesion of the group, and in some cases moving in a certain direction. Can we develop an agent-based model with a simple set of individual movement rules that would allow for all these demands to be met?
This was inspired by a piece of Planet Earth footage on caribou: go to http://dsc.discovery.com/convergence/planet-earth/video-player/video-player.html, scroll down in the video clips to "Planet Earth: Plains: Following the Caribou" and watch the dynamics at about 1:30-2:00. (If anyone has a hard copy of this segment or knows how to get one, please let me know!). In this case each individual caribou pauses to eat along the way but the group never fragments and in fact it seems to almost 'flow' through an area. My guess is that one of the physicists could provide some interesting insight on how to model this.
Daniel Wuellner: Cool idea. Most importantly: I actually brought the Planet Earth DVDs with me which I'll happily lend; maybe we can organize a viewing w/ a projector somewhere.
- Roozbeh Daneshvar: Daniel, I am absolutely in for such a preview. Can you upload it in After Hours so that we all watch it together?
I think there's some swarm literature out there for ideas on rules you could extend to incorporate foraging (or any other caribouish behavior). The one I know is Flocks, herds and schools: A distributed behavioral model (this actually might be the 'original' swarm paper).
Kate Behrman: I also interested in this. One possible extension could be to consider how the structure of the landscape between the two locations affects the movement of the group.
Murad Mithani: It sounds similar to what happens when the cognitive processes are focused on a particular problem to come up with ideas. The initiation of problem solving is a conscious mechanism that flourishes when that initial push is taken away. If you guys are planning to model this in some way, count me in.
Steven Lade: I like the sound of this too. Dare I suggest a meeting, perhaps one lunchtime, to flesh out plans a little more? Allison, since it was your idea, would you like to call it?
Allison Shaw: Sure, that would be great! How about lunch tomorrow (Tuesday the 16th)? Let's try to synchronize sitting together. I talked to JP about doing a Planet Earth showing and he said we could use the projector for the lectures, but we'd need to get a decent set of speakers (as far as I know there isn't a working TV/DVD combination in any of the lounges and we'd have to pay to use the more advanced media system in the lecture room).