Economic Geography and State Emergence

Explanation

The goal of the project is to test the hypothesis that the economic behaviors proposed by Paul Krugman's "New Economic Geography" framework can explain hierarchically organized settlement networks in emergent state societies. Our test will apply Krugman's model and knowledge of caloric resource distributions to an agent-based model that attempts to reproduce the settlement and network structures observed in the Tiwanaku and Roman empires. Our test will help to clarify the degree to which economic networks create a context for the emergence of social competition and inequality. This page is intended to facilitate the project's progress, and is organized with the a final paper structure in mind.

Introduction to New Economic Geography

We intend to explain settlement pattern changes in the Lake Titicaca Basin from 2500 BCE to 1000 CE by employing a variant of an economic model called the "New Economic Geography" by Krugman, 1991, Fujita, et al 1999. The model explains settlement change by balancing forces that encourage production to simultaneously concentrate and disperse. The centrifugal forces that encourage dispersed production come from the uniformly distributed farming population which demands goods. Transportation costs mean that production should be close to farmers and therefore dispersed across the landscape to serve farmers efficiently. Following Krugman and Samuelson, we employ transportation costs that "melt away" a certain proportion of the traded goods to avoid explicitly modeling a transport sector. In addition, we assume that increasing returns to scale obtain for production, meaning that larger production facilities can produce at lower marginal costs. This centripetal force encourages production to be centered in one area. However, production centered in one area attracts more workers and increases local product demand increasing further agglomeration of production.

Our application of Krugman's model intends to expand the types of societies for which the model can be used. Indeed, we find that one of the main empirical regularities of settlement patterns - Zipf's law in city sizes - applies to both industrial and pre-industrial societies. Our model differs from Krugman, et al by including stochastic agricultural production, allowing both agricultural and industrial products to have transportation costs, and producing dynamics through fertility and (at least initially) abstracting away from migration. The other major change is that we conceptualize "manufactured goods" as all goods and services not produced by the agricultural sector. This sector's dominant service is modeled as food trade to reduce a region's food shortfall during bad harvest years. We argue that both manufacturing services and trade services are still subject to increasing returns to scale (through fixed costs and informational spillovers for clustered traders) and constant returns to scale for agriculture.

Introduction to Tiwanaku Empire Settlement Hierearchies

As a state-level society that emerged in-situ, the Tiwanaku Empire presents an ideal case for exploring the role economic geography plays in structuring hierarchically organized societies. From a relatively even distribution of Early Formative Period (ca. 2000-1300 B.C.) small hamlets arose the increasingly nucleated regional centers of the Middle Formative Period (ca. 1300-500 B.C.). Stanish (2003) identifies at least 13 such centers in an incomplete sample. During the Upper Formative Period (ca. 500 B.C. - A.D. 400), two regional centers--Pucara and Tiwanaku/Chiripa--grew an order of magnitude larger than any of the other centers. Finally, by A.D. 400, the urban capital of Tiwanaku emerged as the largest occupational center with a core population somewhere between 30 and 60,000 inhabitants. At it's peak, Tiwanaku settlements were organized roughly as a geographically nested hierarchy (McAndrews et al. 1997). By A.D. 1000, the Tiwanaku Empire, which had become a conquest state, began to collapse.

Attendant to the demographic changes witnessed in the rise of the Tiwanaku Empire were clear economic and politico-religious changes. During the Middle Formative Period, ceramic production becomes more specialized in the regional centers. The Yaya-Mama stylistic tradition also emerges and is manifest in the design of stone statues, or stelae, that are concentrated in the regional centers. Stanish (2003) argues that this new tradition is tied to elites and a pan-regional ideology. In the Upper Formative Period, communal architecture such as sunken courts and artificial mountains, or pyramids, appear at the regional centers. Janusek (2006) argues that architectural design and icongraphy at Tiwanaku was designed to co-opt the power of nature and integrate diverse cultural groups. He further suggests that Tiwanaku's success in "outcompeting" other regional centers stems from its uniquely integrative religious tradition.

Stanish (2003) hypothesizes that population centers are located as a function of resource access and peer polity competition and conflict. To test the idea, Griffin and Stanish (2007) created an agent-based model wherein agricultural productivity, migration, competition, and trade contribute to differential population aggregation. The model does a good job of approximating the empirical distributions, but the ABM's complexity makes it difficult to assess the degree to which any given factor drives the pattern. Our approach, then, will serve to clarify the degree to which formal economic processes drove the emergence of Tiwanaku, and created a context for the development of the elaborate social, political, and religious traditions that characterize Tiwanaku.

Implementing a Spatial Model of the New Economic Geography

Figure 1. Model space for the Tiwanaku Empire test case. The blue area is Lake Titicaca, and the green area shows arable land below 4000 masl.

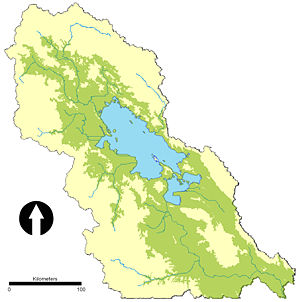
• Environmental Parameters
  • Agricultural productivity: 105-1892 kcal/ha/yr. These figures are derived from Griffin and Stanish (2007:Table A-2) as follows: For each of the five agricultural strategies, the table reports the number of days fallow, caloric yields (kcal/ha), and production costs (person-days/ha. We first adjust the productivity estimates to factor in fallow time. Unfortunately, Griffin and Stanish do not report how many years a field remains productive--only how long it must be fallow. Accordingly, the agricultural yields are multiplied by 1/8 or 1/5 depending on the published fallow values. In order to convert these values into net yields/ha, we next convert the production costs to caloric costs assuming 1 person day equals 2 kcal. For each agricultural strategy, this value is subtracted to from the adjusted yields to derive the net kcal/ha reported above. How these values will vary over time and space will be discussed.
  • Geometry: Figure 1 shows the 28,000 square kilometers of arable land in the Titicaca Basin. This area comprises approximately 35% of the watershed area included in this study. The geo-spatial data are derived from Shuttle Radar Topography Mission data. Projected in a UTM system, the cell size of the data is approximately 91m. The arable land excludes the lake and any cells above 4000m, which is generally accepted to be the point at which the growing season is too short for agriculture.
  • Other: Elevation, distance from lake, and distance from lakes and rivers are other datasets we have at our disoposal.
• Agent Behavior
  • average hunter-gatherer group size: 25 (Kelly 2007:205-213). This provides a justification for setting initial group sizes. Kelly's review suggests that 25 offers an optimal tradeoff between reproductive viability and resource sustainability.
  • average minimum territory size: 10-174 ha. If we assume that an average individual requires 730 kcal/year, then an average village would require approximately 18,250 kcal/year necessitating between 10 and 174 ha.
  • Average birth rate: .81-8.5 children/lifetime(Kelly 2007:Table 6.4) Agriculturalists average 6.6 children/lifetime--slightly higher total fertility rates than hunter-gatherers and horticulturalists (Kelly 2007).
  • Transportation cost
    • human transport: ~20kg/person, 40km/day assuming 5 km/hr on zero slope (Gorenflo and Gale 1990) and 8 hours of travel/day.
    • llama transport: =<25kg/llama (Kuznar 1991)

References

Fujita, M., Krugman, P. and Venables, AJ. 1999. The Spatial Economy. MIT Press.

Gorenflo, L.J., and Nathan Gale 1990 Mapping Regional Settlement in Information Space. Journal of Anthropological Archaeology 9:240-274.

Griffin, Arthur F., and Charles Stanish 2007 An Agent-Based Model of Prehistoric Settlement Patterns and Political Consolidation. Structure and Dynamics: eJournal of Anthropological and Related Sciences 2(2):1-47.

Gumerman, George J., Alan C. Swedlund, Jefferey S. Dean, and Joshua M. Epstein 2003 The Evolution of Social Behavior in the Prehistoric American Southwest. Artificial Life 9:435-444.

Kelly, Robert L. 2007 The Foraging Spectrum. Percheron Press, Clinton Corners.

Krugman, Paul 1991 Increasing Returns and Economic Geography. Journal of Political Economy 99(3):483-499.

Kuznar, Lawrence 1991 Herd Composition in an Ayamara Community of the Peruvian Altiplano: A Linear Programming Problem. Human Ecology 19(3):369-387.

Janusek, John Wayne 2006 The Changing 'Nature' of Tiwanaku Religion and the Rise of an Andean State. World Archaeology 38(3):469-492.

McAndrews, Tomothy, Juan Albarracin-Jordan, and Marc Bermann 1997 Regional Settlement Patterns in the Tiwanaku Valley of Bolivia. Journal of Field Archaeology 24:68-83.

Rauch, Jonathan 2002 Seeing Around Corners. The Atlantic Monthly, April:35-48.

Stanish, Charles 2003 Ancient Titicaca: The Evolution of Complex Society in Southern Peru and Northern Bolivia. University of California Press, Berkeley.

Original Proposal (Do not Edit)

Economic Geography in the Lake Titicaca Basin

By A.D. 1200, the Tiwanaku Empire reached an apex in population and social complexity. The distribution of settlement sizes at that time approximated a power-law or log-normal distribution with the urban center of Tiwanaku as the capitol. Archaeologists such as Stanish, Janusek, and others have argued that, while economic factors drive early settlement patterns, differential growth in settlements is primarily a function of competing political polities. They argue that polities with the most integrative religious traditions continued to grow relative to surrounding communities. In this project, we wish to explore the possibility that a simpler economic /demographic model can explain the emergence of such settlement patterns through time. Specifically, we intend to follow the general modeling framework created by Paul Krugman, which he calls the “New Economic Geography.”

Our working method would be to use the behaviors proposed by Krugman in an agent-based model that predicts the spatial distributions of the empirical settlement patterns in the Lake Titicaca Basin. The model explains settlement change by assuming that separate forces encourage production to simultaneously concentrate and disperse. The centrifugal forces that encourage dispersed production come from the uniformly distributed farming population which demands goods. Transportation costs mean that production should be close to farmers and therefore dispersed across the landscape to serve farmers efficiently. At the same time, we assume that increasing returns to scale obtains for production, meaning that larger production facilities can produce at lower marginal costs. This centripetal force encourages production to be centered in one area. In addition, production centered in one area attracts more workers and increases local demand for the product. Depending on model parameters, these dynamics can give rise to a dominant production and population centered, as seen in the Lake Titicaca data.

We don’t think we can take this project on by ourselves, so we are writing to see if we can get 1 or 2 more people interested and then move forward. If interested, please talk to Randy Haas or Jeremy Barofsky. Thanks!