Evolutionary dynamics of fitness-driven walkers on a graph
From Santa Fe Institute Events Wiki
Evolutionary dynamics of fitness-driven walkers on a graph
Evolutionary game theory is a theoretical framework that has been widely investigated for modeling in fields as diverse as biology, economics, and sociology. At the same time, in recent years, great attention has been focused on complex networks. In particular, it has been shown that the evolution of strategies of games played on a network does not resemble the one observed in a well-mixed population. Although the frame of complex networks in most contexts is more realistic than a well-mixed interaction, it turns out to be not exact in all situations.
In this project we introduce a model were the two frames of well-mixed population and heterogeneous pattern of interactions are put together and act at different time-scales on the dynamics. In particular, we investigate how strategies of interacting individuals in a group evolve as they are allowed to interact with other agents and migrate to other neighboring groups through a biased random walk. Here, we take into account different kind of network topologies. Each node in a network represents a group of players in a well mixed state. Agents in a group/class then interact with each other playing either one of two strategies, A and B. The population of players using strategies A and B are then evaluated, respectively, allowing us to calculate the average payoff of a group. Each agent then migrates to a particular neighboring node or group through a biased random walk by evaluating and contrasting the different fitness values of its group's neighbors.
This model is reminiscent of social systems and other ecological systems where agents migrate to a neighboring environment depending on the fitness of the said region. In social systems, this may describe how and why individuals would move from one neighboring city to another. This may also tell of why employees of a certain company would want to move to other companies.
(Details to be uploaded soon.)
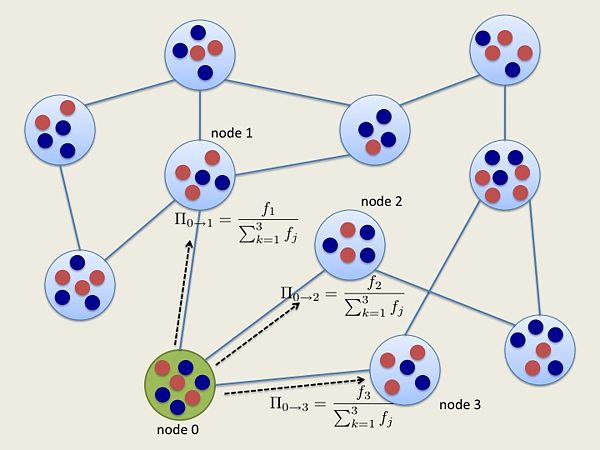
The figure below is a schematic diagram of our proposed model that investigates how strategies of interacting individuals in a group (nodes) evolve as they are allowed to interact with other agents within the group and migrate to other neighboring groups through a biased random walk (relative fitness of the neighboring nodes). The colors of the agents inside the nodes depend on the strategy they are playing. Each of the agents in node 0 then migrates to either nodes 1, 2, or 3, which is governed by the probability $\Pi _{i \rightarrow j}$.
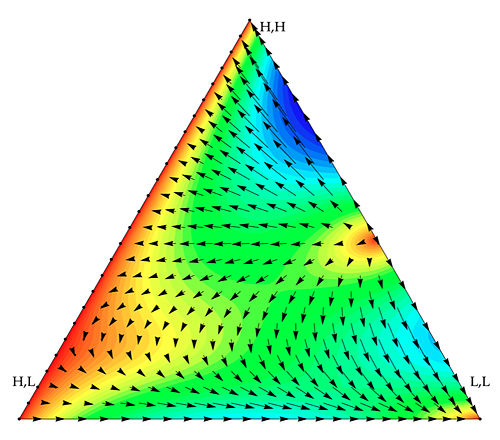
Evolutionary dynamics of the ultimatum game in a well mixed population with three strategies,
1. High proposition, High aspiration (H,H)
2. High proposition, Low aspiration (H,L)
3. Low proposition, Low aspiration (L,L)
The triangle is the simplex where the dynamics of the system reside. The vertices denote that the population consists completely of the labeled strategy and the interior is a mixture of all the three strategies at different frequencies. An unstable point exists on the face of the simplex joining Strategy 1 and 3. Strategy 2 and 1 are neutral with respect to each other.
