Robustness of complex networks (project): Difference between revisions
From Santa Fe Institute Events Wiki
| Line 36: | Line 36: | ||
# [[Ian Wood]] - ibwood@indiana.edu | # [[Ian Wood]] - ibwood@indiana.edu | ||
# [[Xin Lu]] - xin.lu@ki.se | # [[Xin Lu]] - xin.lu@ki.se | ||
== BA algorithm in Python == | |||
''Caution! when you copy this to the Python delete one space from the first line, i.e., before def'' | |||
def barabasi_albert_graph(n, m, seed=None): | |||
"""Return random graph using Barabási-Albert preferential attachment model. | |||
A graph of n nodes is grown by attaching new nodes each with m | |||
edges that are preferentially attached to existing nodes with high | |||
degree. | |||
Parameters | |||
---------- | |||
n : int | |||
Number of nodes | |||
m : int | |||
Number of edges to attach from a new node to existing nodes | |||
seed : int, optional | |||
Seed for random number generator (default=None). </br> | |||
Returns | |||
------- | |||
G : Graph | |||
Notes | |||
----- | |||
The initialization is a graph with with m nodes and no edges.</br> | |||
References | |||
---------- | |||
.. [1] A. L. Barabási and R. Albert "Emergence of scaling in | |||
random networks", Science 286, pp 509-512, 1999. | |||
"""</br> | |||
if m < 1 or m >=n: | |||
raise nx.NetworkXError(\ | |||
"Barabási-Albert network must have m>=1 and m<n, m=%d,n=%d"%(m,n)) | |||
if seed is not None: | |||
random.seed(seed) </br> | |||
# Add m initial nodes (m0 in barabasi-speak) | |||
G=empty_graph(m) | |||
G.name="barabasi_albert_graph(%s,%s)"%(n,m) | |||
# Target nodes for new edges | |||
targets=list(range(m)) | |||
# List of existing nodes, with nodes repeated once for each adjacent edge | |||
repeated_nodes=[] | |||
# Start adding the other n-m nodes. The first node is m. | |||
source=m | |||
while source<n: | |||
# Add edges to m nodes from the source. | |||
G.add_edges_from(zip([source]*m,targets)) | |||
# Add one node to the list for each new edge just created. | |||
repeated_nodes.extend(targets) | |||
# And the new node "source" has m edges to add to the list. | |||
repeated_nodes.extend([source]*m) | |||
# Now choose m unique nodes from the existing nodes | |||
# Pick uniformly from repeated_nodes (preferential attachement) | |||
targets = _random_subset(repeated_nodes,m) | |||
source += 1 | |||
return G | |||
Revision as of 04:13, 11 June 2012
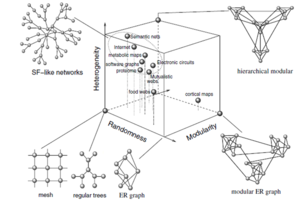
Problem statement
Complex networks have various properties which can be measured in real networks (WWW, social networks, biological networks), e.g. degree distribution, modularity, hierarchy, assortativity etc. Robustness of complex networks is a big question, however only some progress have been done in this direction. For example, it was shown that the scale-free networks are much more topologically robust to random attacks than random networks. Many people claim that various characteristics of complex networks will influence the robustness interdependently. The question I am interested in is how?
Approach
The idea is to generate continuous topology space of various complex networks (networks with different modularity, degree distribution, hierarchy etc) and use it to measure their robustness (see Fig. 1). There are many approaches to measure the robustness of complex networks. For example we can remove edges of vertices of a complex network graph and look at the size of a giant cluster. We can discuss other possibilities.
If you are interested you can contact me directly or via my E-mail: krystoferivanov@gmail.com or via my discussion page in CSSS 2012 wiki.
Relevant literature
- Important papers about network generation are highlighted in bold
- BA Scale-free network
- How to generate Scale-free modular network using preferential attachment
- Scale-free networks with tunable degree distribution exponents
- Scale free networks with tunable clustering
- Error and attack tollerance of complex networks
- Structural Robustness of Complex networks
- Assortative mixing in networks
- Mean field theory to study scale-free networks
- Kroneker Graphs
- Exact maximum-likelihood method to detect patterns in real networks
- Biological robustness
- Attack vulnerability of complex networks
- Supply Network Topology and Robustness against Disruptions – an investigation using multi agent model
- Random graphs with arbitrary degree distributions and their applications
- Resolution limit in community detection - about a typical modularity measure and its limitations
- Add a relevant paper...
Learning Python
Participants
- Oleksandr Ivanov - krystoferivanov@gmail.com
- Ian Wood - ibwood@indiana.edu
- Xin Lu - xin.lu@ki.se
BA algorithm in Python
Caution! when you copy this to the Python delete one space from the first line, i.e., before def
def barabasi_albert_graph(n, m, seed=None):
"""Return random graph using Barabási-Albert preferential attachment model.
A graph of n nodes is grown by attaching new nodes each with m
edges that are preferentially attached to existing nodes with high
degree.
Parameters
----------
n : int
Number of nodes
m : int
Number of edges to attach from a new node to existing nodes
seed : int, optional
Seed for random number generator (default=None).
Returns
-------
G : Graph
Notes
-----
The initialization is a graph with with m nodes and no edges.
References
----------
.. [1] A. L. Barabási and R. Albert "Emergence of scaling in
random networks", Science 286, pp 509-512, 1999.
"""
if m < 1 or m >=n:
raise nx.NetworkXError(\
"Barabási-Albert network must have m>=1 and m<n, m=%d,n=%d"%(m,n))
if seed is not None:
random.seed(seed)
# Add m initial nodes (m0 in barabasi-speak)
G=empty_graph(m)
G.name="barabasi_albert_graph(%s,%s)"%(n,m)
# Target nodes for new edges
targets=list(range(m))
# List of existing nodes, with nodes repeated once for each adjacent edge
repeated_nodes=[]
# Start adding the other n-m nodes. The first node is m.
source=m
while source<n:
# Add edges to m nodes from the source.
G.add_edges_from(zip([source]*m,targets))
# Add one node to the list for each new edge just created.
repeated_nodes.extend(targets)
# And the new node "source" has m edges to add to the list.
repeated_nodes.extend([source]*m)
# Now choose m unique nodes from the existing nodes
# Pick uniformly from repeated_nodes (preferential attachement)
targets = _random_subset(repeated_nodes,m)
source += 1
return G
